Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
A. z=a+bi hoặc z=-a-bi (loại)
B. ![]() (loại)
(loại)
C. giải phương trình bậc hai ẩn z có nghiệm z=a+bi; z=a-bi (thỏa mãn)

\(\Delta=b^2-4ac\Rightarrow\left\{{}\begin{matrix}z_1=\dfrac{-b-i\sqrt{4ac-b^2}}{2a}\\z_2=\dfrac{-b+i\sqrt{4ac-b^2}}{2a}\end{matrix}\right.\Rightarrow\left|z_1+z_2\right|^2=\dfrac{b^2}{a^2};\left|z_1-z_2\right|^2=\dfrac{4ac-b^2}{a^2}\)
\(\Rightarrow P=\dfrac{4c}{a}\) => C

Chắc bạn ghi nhầm đề \(z_1\overline{z_2}+\overline{z_1}z_2\) mới có lý chứ nhỉ?
Khi pt bậc 2 có 2 nghiệm phức \(z_1;z_2\) thì \(z_1=\overline{z_2}\)
Do đó \(z_1\overline{z_2}+\overline{z_1}z_2=z_1^2+z_2^2=\left(z_1+z_2\right)^2-2z_1z_2=\left(-4\right)^2-2.7=2\)

a) \(2^{x+4}+2^{x+2}=5^{x+1}+3\cdot5^x\)
\(\Rightarrow2^x+2^4+2x^x+2^2=5^x\cdot x+3\cdot5^x\)
\(\Leftrightarrow2^x+16+2^x\cdot4=5\cdot5^x+3\cdot5^x\)
\(\Leftrightarrow16\cdot2^x+4\cdot2^x=8\cdot5^x\)
\(\Leftrightarrow20\cdot2^x=8\cdot5^x\)
\(\Leftrightarrow20\cdot\left(\dfrac{2}{5}\right)^x=8\)
\(\Leftrightarrow\left(\dfrac{2}{5}\right)^x=\dfrac{2}{5}\)
\(\Leftrightarrow\left(\dfrac{2}{5}\right)^x=\left(\dfrac{2}{5}\right)^1\)
\(\Rightarrow x=1\)

\(log\left(5\left(x^2+1\right)\right)\ge log\left(mx^2+4x+m\right)\)
- BPT đúng \(\forall x\Rightarrow log\left(mx^2+4x+m\right)\) xác định \(\forall x\in R\)
\(\Rightarrow mx^2+4x+m>0\) \(\forall x\in R\)
\(\Rightarrow\left\{{}\begin{matrix}a=m>0\\\Delta'=4-m^2< 0\end{matrix}\right.\) \(\Rightarrow m>2\) (1)
- Lại có \(x^2+1\ge1\) \(\forall x\)
\(\Rightarrow5\left(x^2+1\right)\ge mx^2+4x+m\)
\(\Leftrightarrow5\left(x^2+1\right)-4x\ge m\left(x^2+1\right)\)
\(\Leftrightarrow5-\dfrac{4x}{x^2+1}\ge m\)
Đặt \(f\left(x\right)=5-\dfrac{4x}{x^2+1}\Rightarrow f\left(x\right)\ge m\) \(\forall x\Leftrightarrow m\le min\left(f\left(x\right)\right)\)
Ta có \(f\left(x\right)=3+2-\dfrac{4x}{x^2+1}=3+\dfrac{2\left(x-1\right)^2}{x^2+1}\ge3\)
\(\Rightarrow min\left(f\left(x\right)\right)=3\Rightarrow m\le3\) (2)
Kết hợp (1), (2) \(\Rightarrow2< m\le3\Rightarrow m=3\)
Vậy có 1 giá trị nguyên duy nhất của m để BPT đúng với mọi x
Đáp án B

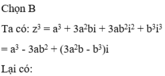
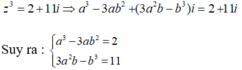



Nếu \(z_1=a+bi\) là nghiệm thì \(z_2=a-bi\) cũng là nghiệm, do đó \(1-i\) cũng là nghiệm
\(\Rightarrow\left\{{}\begin{matrix}-a=z_1+z_2=2\\b=z_1z_2=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-2\\b=2\end{matrix}\right.\)
\(\Rightarrow a-b=-4\)