Phương trình \(x^2-x-3=0\) có 2 nghiệm x\(_1\),x

\(x^2-x-3=0\) có 2 nghiệm x\(_1\),x

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

HY

Hải Yến Lê

14 tháng 7 2021

Phương trình \(x^2-x-3=0\) có 2 nghiệm x\(_1\),x\(_2\).Tính tổng \(S=\dfrac{1}{x1}+\dfrac{1}{x2}\)

#Hỏi cộng đồng OLM #Toán lớp 9

1

TC

Trên con đường thành công không có....

14 tháng 7 2021

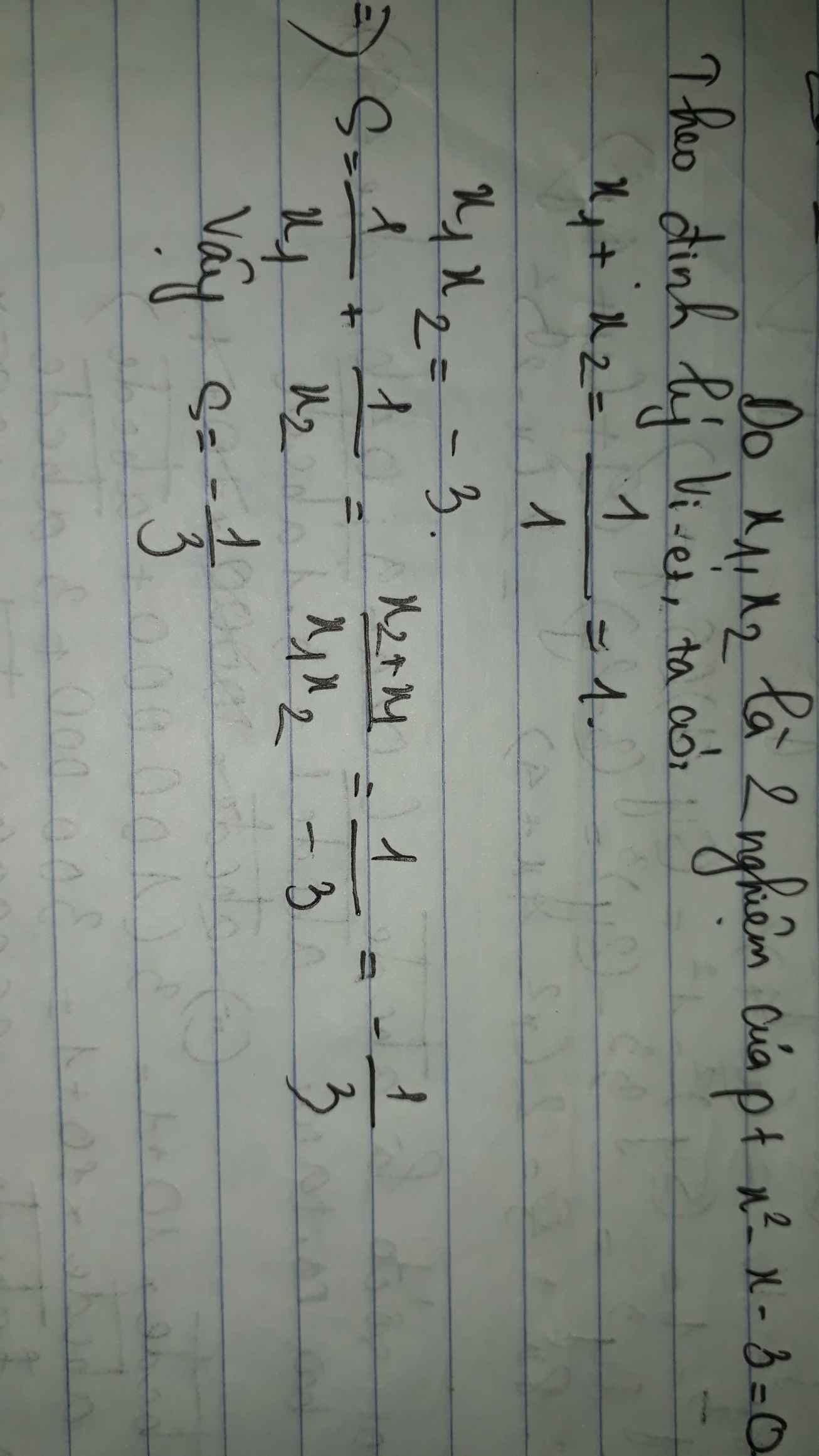
undefined

Các câu hỏi dưới đây có thể giống với câu hỏi trên

LH

Lin-h Tây'x

22 tháng 3 2018

1. Cho phương trình : -3x\(^2\) - 5x - m + 2 = 0. a) m=? để phương trình có hai nghiệm : x\(_1\) = \(\dfrac{1}{3}\)x\(_2\) 2. Cho phương trình : x\(^2\) + 5x + m - 2 = 0 a) m=? để phương trình có hai nghiệm x1, x2 thỏa mãn : x\(_1\)= 2x\(_2\)...

#Hỏi cộng đồng OLM #Toán lớp 9

4

LH

Lin-h Tây'x

22 tháng 3 2018

mọi người giúp e với ạ !!

AH

Akai Haruma

Giáo viên

23 tháng 3 2018

Bài 1:

Ta viết lại phương trình: \(3x^2+5x+(m-2)=0\)

Để pt có hai nghiệm (không nhất thiết phân biệt) thì:

\(\Delta=25-12(m-2)\geq 0\)

\(\Leftrightarrow m\leq \frac{49}{12}\)

Khi đó, áp dụng định lý Viete của pt bậc 2: \(\left\{\begin{matrix} x_1+x_2=-\frac{5}{3}\\ x_1x_2=\frac{m-2}{3}\end{matrix}\right.\)

\(\Leftrightarrow \left\{\begin{matrix} \frac{1}{3}x_2+x_2=\frac{-5}{3}\\ \frac{1}{3}x_2^2=\frac{m-2}{3}\end{matrix}\right.\) (thay \(x_1=\frac{1}{3}x_2\) )

\(\Leftrightarrow \left\{\begin{matrix} x_2=\frac{-5}{4}\\ \frac{1}{3}x_2^2=\frac{m-2}{3}\end{matrix}\right.\) \(\Rightarrow \frac{m-2}{3}=\frac{1}{3}\left(\frac{-5}{4}\right)^2=\frac{25}{48}\)

\(\Leftrightarrow m=\frac{57}{16}\) (thỏa mãn)

Vậy \(m=\frac{57}{16}\)

MC

minh chu Thai

9 tháng 8 2016

1/ cho phương trình : 5x\(^2\)+y\(^2\)+ 4xy + 4x + 2y - 3=0tìm m để phương trình có 2 nghiệm x\(_1\),x\(_2\)thõa mãn điều kiện 5x\(_1\)+2x\(_2\)=42/cho phương trình x\(^2\)+(m-1)x-6=0. tìm m để phương trình có hai nghiệm x\(_1\),x\(_2\)sao cho A=(x\(_1\)\(^2\)-9)(x\(_2\)\(^2\)-4) đạt giá trị lơn...

#Hỏi cộng đồng OLM #Toán lớp 9

0

JV

Jessica Võ

16 tháng 5 2020

cho phương trình: \(x^2\ -2mx\) + 2m - 2

Khi phương trình có 2 nghiệm phân biệt x\(_1\), x\(_2\) hãy viết công thức tính hai nghiệm đó theo m để (x\(_1\)+x\(_2\))\(^2\)=3+2x\(_1\)x\(_2\)

#Hỏi cộng đồng OLM #Toán lớp 9

0

LH

Lin-h Tây'x

22 tháng 3 2018

Cho phương trình : ( m- 1 ). x\(^2\) - 3x + 2 = 0
a) m= ? để phương trình đã cho có hai nghiệm x\(_1\), x\(_2\) thỏa mãn : \(\dfrac{1}{x_1}\) + \(\dfrac{1}{x_2}\) =3

#Hỏi cộng đồng OLM #Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

26 tháng 6 2022

TH1: m=1

Pt sẽ là -3x+2=0

hay x=2/3(loại)

TH2: m<>1

\(\text{Δ}=\left(-3\right)^2-4\left(m-1\right)\cdot2=9-8\left(m-1\right)=-8m+17\)

Để phương trình có hai nghiệm thì -8m+17>=0

hay m<=17/8

Ta có: \(\dfrac{1}{x_1}+\dfrac{1}{x_2}=3\)

\(\Leftrightarrow\dfrac{x_1+x_2}{x_1x_2}=3\)

\(\Leftrightarrow\dfrac{3}{m-1}=3\cdot\dfrac{2}{m-1}=\dfrac{6}{m-1}\)(vô lý)

HN

Hoàng Ngọc Tuyết Nhung

27 tháng 7 2018 - olm

cho phương trình :2x\(^2\)+(2m−1)x+m−1=0\(1)a) xác định m để (1) có 2 nhiệm x\(_1\),x\(_2\) thỏa 3x\(_1\)−4x\(_2\)=11b)xác định m để (1) có 2 nghiệm đều dươngc) tìm hệ thức giữa x\(_1\),x\(_2\) không phụ thuộc vào...

#Hỏi cộng đồng OLM #Toán lớp 9

0

TH

Trần Hạo Thiên

14 tháng 5 2020

Cho phương trình x\(^2\)-mx+m-1=0 a) CMinh phương trình luôn có nghiệm với mọi m b) Tìm m để phương trình có nghiệm số kép c) Cho A = x\(_1\)\(^2\)+x\(_2\)\(^2\)-6x\(_1\).x\(_2\) với x1 và x2 là nghiệm của phương trình. Biểu diễn A theo m ...

#Hỏi cộng đồng OLM #Toán lớp 9

0

TH

Trần Hạo Thiên

14 tháng 5 2020

Cho phương trình x\(^2\)+3x+m=0, không giải phương trình Trong trường hợp phương trình có nghiệm x\(_1\)và x\(_2\). Tìm m biết a) x\(_1\)-x\(_2\)=6 b) 3x\(_1\)+2x\(_2\)=20 c) x\(_1\)\(^2\)-x\(_2\)\(^2\)=34 d) x\(_1\)=2x\(_2\) e)...

#Hỏi cộng đồng OLM #Toán lớp 9

1

NV

Nguyễn Việt Lâm

Giáo viên

14 tháng 5 2020

\(\Delta=9-4m\ge0\Rightarrow m\le\frac{9}{4}\)

Theo Viet: \(\left\{{}\begin{matrix}x_1+x_2=-3\\x_1x_2=m\end{matrix}\right.\)

a/ \(\left\{{}\begin{matrix}x_1-x_2=6\\x_1+x_2=-3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=\frac{3}{2}\\x_2=-\frac{9}{2}\end{matrix}\right.\)

\(x_1x_2=m\Rightarrow m=\frac{3}{2}.\left(-\frac{9}{2}\right)=-\frac{27}{4}\)

b/ \(\left\{{}\begin{matrix}3x_1+2x_2=20\\x_1+x_2=-3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=26\\x_2=-29\end{matrix}\right.\)

\(\Rightarrow m=x_1x_2=-29.26=-754\)

c/ \(\left\{{}\begin{matrix}\left(x_1-x_2\right)\left(x_1+x_2\right)=34\\x_1+x_2=-3\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_1-x_2=-\frac{34}{3}\\x_1+x_2=-3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=-\frac{43}{6}\\x_2=\frac{25}{6}\end{matrix}\right.\) \(\Rightarrow m=-\frac{1075}{36}\)

d/ \(\left\{{}\begin{matrix}x_1=2x_2\\x_1+x_2=-3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_2=-1\\x_1=-2\end{matrix}\right.\) \(\Rightarrow m=2\)

e/ Giống câu c, bạn tự giải

H

Huyền

3 tháng 3 2018

Cho pt: x\(^2\) - 2mx + m\(^2\) -1 = 0

a, Giải phương trình khi m=2

b, Tìm m để phương trình có hai nghiệm phân biệt x\(_1\), x\(_2\) thỏa mãn \(\dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{1}{2}\)

#Hỏi cộng đồng OLM #Toán lớp 9

2

AH

Akai Haruma

Giáo viên

4 tháng 3 2018

Lời giải:

a)

Khi $m=2$ phương trình trở thành:

\(x^2-2.2x+2^2-1=0\)

\(\Leftrightarrow x^2-4x+3=0\Leftrightarrow (x-1)(x-3)=0\)

\(\Leftrightarrow \left[\begin{matrix} x=1\\ x=3\end{matrix}\right.\)

b)

Để pt có hai nghiệm phân biệt thì:

\(\Delta'=m^2-(m^2-1)>0\Leftrightarrow 1>0\) (luôn đúng với mọi số thực $m$)

Khi đó áp dụng hệ thức Viete có: \(\left\{\begin{matrix} x_1+x_2=2m\\ x_1x_2=m^2-1\end{matrix}\right.\)

Do đó: \(\frac{1}{x_1}+\frac{1}{x_2}=\frac{1}{2}\)

\(\Leftrightarrow \frac{x_1+x_2}{x_1x_2}=\frac{1}{2}\Leftrightarrow \frac{2m}{m^2-1}=\frac{1}{2}\)

\(\Rightarrow m^2-1=4m\Leftrightarrow m^2-4m-1=0\)

\(\Leftrightarrow (m-2)^2=5\Rightarrow \left[\begin{matrix} m=2+\sqrt{5}\\ m=2-\sqrt{5}\end{matrix}\right.\) (đều chọn)

N

ngonhuminh

6 tháng 3 2018

a) đơn giản (bước đệm làm b thôi

b) m thỏa mãn đồng thời hệ \(\left\{{}\begin{matrix}f\left(0\right)\ne0\\\Delta>0\\\dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{1}{2}\end{matrix}\right.\)\(\begin{matrix}\left(1\right)\\\left(2\right)\\\left(3\right)\end{matrix}\)

\(\left(1\right)\Leftrightarrow0-0+m^2-1\ne0\Leftrightarrow m\ne\left\{\pm1\right\}\)

\(\left(2\right)\Leftrightarrow\Delta'_{\left(x\right)}=m^2-m^2+4=4>0\forall m\Rightarrow m\in R\backslash\left\{\pm1\right\}\)

\(\left(3\right)\Leftrightarrow\dfrac{x_2+x_1}{x_1.x_2}=\dfrac{1}{2}\)

với đk m<=> \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1.x_2=m^2-1\\2\left(x_1+x_2\right)=x_1.x_2\end{matrix}\right.\)\(\Leftrightarrow m^2-4m-1=0\)

\(\Delta'_{\left(m\right)}=2^2+1=5\Rightarrow m=2\pm\sqrt{5}\) thỏa mãn đk m nhận

LG

Lê Gia Phong

18 tháng 3 2018

Cho phương trình: x\(^2\)-2(m-1)x+m\(^2\)-3(với m là thang số) a,Tìm m để phương trình có 2 nghiệm x\(_1\),x\(_2\) thỏa mãn : x\(_1\)-x\(_2\)\(=\)2 b,Tìm m để phương trình có 2 nghiệm x\(_1\),x\(_2\) thỏa mãn : x\(_1\)x\(_2\)-x\(_1\)-x\(_2\)\(=\)11 c,Trong trường hợp có 2 nghiệm x\(_1\),x\(_2\),hãy tìm 1 hệ thức liên kết giữa 2 nghiệm của phương trình không phụ thuộc vào m. Mong mọi người giúp đỡ.Ai nhanh mà đúng...

#Hỏi cộng đồng OLM #Toán lớp 9

0

LG

Lê Gia Phong

18 tháng 3 2018

Câu hỏi hay

Cho phương trình: x\(^2\)-2(m-1)x+m\(^2\)-3(với m là thang số) a,Tìm m để phương trình có 2 nghiệm x\(_1\),x\(_2\) thỏa mãn : x\(_1\)-x\(_2\)\(=\)2 b,Tìm m để phương trình có 2 nghiệm x\(_1\),x\(_2\) thỏa mãn : x\(_1\)x\(_2\)-x\(_1\)-x\(_2\)\(=\)11 c,Trong trường hợp có 2 nghiệm x\(_1\),x\(_2\),hãy tìm 1 hệ thức liên kết giữa 2 nghiệm của phương trình không phụ thuộc vào m. Mong mọi người giúp đỡ.Ai nhanh mà đúng...

#Hỏi cộng đồng OLM #Toán lớp 9

1

AH

Akai Haruma

Giáo viên

18 tháng 3 2018

Lời giải:

Để pt có hai nghiệm phân biệt thì \(\Delta'=(m-1)^2-(m^2-3)>0\)

\(\Leftrightarrow 4-2m>0\Leftrightarrow m< 2\)

Khi đó áp dụng định lý Viete về pt bậc 2: \(\left\{\begin{matrix} x_1+x_2=2(m-1)\\ x_1x_2=m^2-3\end{matrix}\right.(*)\)

a) \(x_1-x_2=2\Rightarrow (x_1-x_2)^2=4\)

\(\Leftrightarrow x_1^2+x_2^2-2x_1x_2=4\Leftrightarrow x_1^2+x_2^2+2x_1x_2-4x_1x_2=4\)

\(\Leftrightarrow (x_1+x_2)^2-4x_1x_2=4\)

\(\Leftrightarrow 4(m-1)^2-4(m^2-3)=4\)

\(\Leftrightarrow 8m=12\Leftrightarrow m=\frac{3}{2}\) (thỏa mãn)

b) \(x_1x_2-x_1-x_2=11\)

\(\Leftrightarrow x_1x_2-(x_1+x_2)=11\)

\(\Leftrightarrow m^2-3-2(m-1)=11\)

\(\Leftrightarrow m^2-2m-12=0\Leftrightarrow \left[\begin{matrix} m=1+\sqrt{13}\\ m=1-\sqrt{13}\end{matrix}\right.\)

Vì \(m<2\Rightarrow m=1-\sqrt{13}\)

c)Ta có: \(\left\{\begin{matrix} x_1+x_2=2(m-1)\\ x_1x_2=m^2-3\end{matrix}\right.\)

\(\Rightarrow \left\{\begin{matrix} x_1+x_2+2=2m\\ x_1x_2+3=m^2\end{matrix}\right.\)

Suy ra \( (x_1+x_2+2)^2=4(x_1x_2+3)(=4m^2)\)

\(\Leftrightarrow x_1^2+x_2^2+4+2x_1x_2+4(x_1+x_2)=4x_1x_2+12\)

\(\Leftrightarrow x_1^2+x_2^2-2x_1x_2+4(x_1+x_2)-8=0\)

Đây chính là biểu thức (không phụ thuộc m) cần tìm.

LG

Lê Gia Phong

21 tháng 3 2018

Cảm ơn cô (thầy) ạ!