Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

phương trình vô nghiệm:
\(\Delta'< 0\Leftrightarrow\left(m+1\right)^2-4< 0\Leftrightarrow-2< m-1< 2\Leftrightarrow-1< m< 3\)

a: \(\Leftrightarrow px-2=0\)
Để phương trình vô nghiệm thì p=0
b: \(\Leftrightarrow x\left(p^2-4\right)=p-2\)
Để phương trình có vô số nghiệm thì p-2=0
hay p=2

Cho phương trình 2x^4 - (m - 1)x^2+m-3=0Tìm điều kiện của m để phương trình có 4 nghiệm phân biệt - H
anh vào link này nếu không vào được thì liên hệ em
@mlem

Làm theo cách lớp 8 :
Theo đề bài ta có hệ phương trình : \(\left\{{}\begin{matrix}7x-5y=9\left(1\right)\\14x-10y=10\left(2\right)\end{matrix}\right.\)
Ta thấy, lấy vế trái của phương trình (1) nhân với 2 ta được : \(\left(7x-5y\right)\cdot2=14x-10y\) => trùng với vế trái của phương trình (2).
Tiếp tục ta lấy vế phải của phương trình (1) nhân với 2 ta được \(9\cdot2=18\ne\) với kết quả của vế trái phương trình (2) = 10.
Vậy ta kết luận hệ phương trình vô nghiệm.

Đáp án: A
Bước 1 sai vì giả sử phản chứng sai, phải giả sử phương trình vô nghiệm và a, c trái dấu.

Lời giải:
PT $\Leftrightarrow (x+1)^2+|x+1|-(m+1)=0$
$\Leftrightarrow |x+1|^2+|x+1|-(m+1)=0$
Đặt $|x+1|=t(t\geq 0)$ thì: $t^2+t-(m+1)=0(*)$
Với $m=1$ thì $t^2+t-2=0$
$\Leftrightarrow (t-1)(t+2)=0$
Vì $t\geq 0$ nên $t=1\Leftrightarrow |x+1|=1$
$\Leftrightarrow x+1=\pm 1\Leftrightarrow x=0$ hoặc $x=-2$
Để pt vô nghiệm thì $(*)$ chỉ có nghiệm âm hoặc vô nghiệm.
PT $(*)$ chỉ có nghiệm âm khi \(\left\{\begin{matrix} \Delta (*)=1+4(m+1)\geq 0\\ S=-1< 0\\ P=-(m+1)<0\end{matrix}\right.\Leftrightarrow m>-1\)
Để $(*)$ vô nghiệm khi $\Delta=4m+5< 0$
$\Leftrightarrow m< \frac{-5}{4}$
Vậy $m>-1$ hoặc $m< \frac{-5}{4}$

a) Phương trình vô nghiệm:
\(\Leftrightarrow\Delta'< 0\)\(\Leftrightarrow\left(3m-1\right)^2-3\left(3m^2-m-1\right)< 0\)
\(\Leftrightarrow3m+4< 0\)\(\Leftrightarrow m< \dfrac{-4}{3}\).
b) Thay \(m=-1\) vào phương trình ta có:
\(3x^2+2\left(3.1-1\right)x+3.1^2-1-1=0\)\(\Leftrightarrow3x^2+2x-1=0\)
Do \(a-b+c=0\) nên phương trình có một nghiệm \(x=-1\), một nghiệm \(x=\dfrac{1}{3}\).

Bất phương trình 2x+y > 3 là bất phương trình bậc nhất hai ẩn và có vô số nghiệm.
Chọn C.

Ta có:
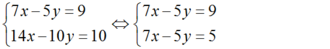
Không tồn tại cặp nghiệm (x ; y) nào thỏa mãn hệ phương trình trên nên hệ phương trình đã cho vô nghiệm.
LÂU MÁY BỊ LỔI
phương trình vô nghiệm là : một trong những dạng toán tương đối khó với nhiều học sinh.
ví dụ :
: Tìm m để phương trình 5x2-2x+m=0 vô nghiệm