Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

3x2 + 8x + 2 = 0
Có a = 3; b' = 4; c = 2
⇒ Δ’ = 42 – 2.3 = 10 > 0
⇒ Phương trình có hai nghiệm phân biệt:


* Chứng minh:
Phương trình a x 2 + b x + c = 0 có hai nghiệm x 1 ; x 2
⇒ Theo định lý Vi-et: 
Khi đó : a.(x – x1).(x – x2)
= a.(x2 – x1.x – x2.x + x1.x2)
= a.x2 – a.x.(x1 + x2) + a.x1.x2
= 
= a . x 2 + b x + c ( đ p c m ) .
* Áp dụng:
a) 2 x 2 – 5 x + 3 = 0
Có a = 2; b = -5; c = 3
⇒ a + b + c = 2 – 5 + 3 = 0
⇒ Phương trình có hai nghiệm 
Vậy: 
b) 3 x 2 + 8 x + 2 = 0
Có a = 3; b' = 4; c = 2
⇒ Δ ’ = 4 2 – 2 . 3 = 10 > 0
⇒ Phương trình có hai nghiệm phân biệt:


* Chứng minh:
Phương trình ax2 + bx + c = 0 có hai nghiệm x1; x2
⇒ Theo định lý Vi-et: 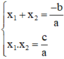
Khi đó : a.(x – x1).(x – x2)
= a.(x2 – x1.x – x2.x + x1.x2)
= a.x2 – a.x.(x1 + x2) + a.x1.x2
= 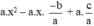
= a.x2 + bx + c (đpcm).
* Áp dụng:
a) 2x2 – 5x + 3 = 0
Có a = 2; b = -5; c = 3
⇒ a + b + c = 2 – 5 + 3 = 0
⇒ Phương trình có hai nghiệm 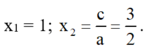
Vậy: 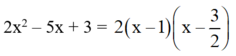

a)\(\sqrt{3x+1}+2x=\sqrt{x-4}-5\left(ĐKXĐ:x\ge4\right)\)
\(\Leftrightarrow\left(\sqrt{3x+1}-\sqrt{x-4}\right)+\left(2x+5\right)=0\)
\(\Leftrightarrow\frac{3x+1-x+4}{\sqrt{3x+1}+\sqrt{x-4}}+\left(2x+5\right)=0\)
\(\Leftrightarrow\frac{2x+5}{\sqrt{3x+1}+\sqrt{x-4}}+\left(2x+5\right)=0\)
\(\Leftrightarrow\left(2x+5\right)\left(\frac{1}{\sqrt{3x+1}+\sqrt{x-4}}+1\right)=0\)
a') (tiếp)
\(\Leftrightarrow\orbr{\begin{cases}2x+5=0\\\frac{1}{\sqrt{3x+1}+\sqrt{x-4}}+1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-2,5\left(KTMĐKXĐ\right)\\\frac{1}{\sqrt{3x+1}+\sqrt{x-4}}+1=0\end{cases}}\)
Xét phương trình \(\frac{1}{\sqrt{3x+1}+\sqrt{x-4}}+1=0\)(1)
Với mọi \(x\ge4\), ta có:
\(\sqrt{3x+1}>0\); \(\sqrt{x-4}\ge0\)
\(\Rightarrow\sqrt{3x+1}+\sqrt{x-4}>0\Rightarrow\frac{1}{\sqrt{3x+1}+\sqrt{x-4}}>0\)
\(\Rightarrow\frac{1}{\sqrt{3x+1}+\sqrt{x-4}}+1>0\)
Do đó phương trình (1) vô nghiệm.
Vậy phương trình đã cho vô nghiệm.

a) \(x^3-5x^2+\left(2m+5\right)x-4m+2=0\left(1\right)\)\(\Leftrightarrow\left(x-2\right)\left(x^2-3x+2m-1\right)=0\Leftrightarrow\orbr{\begin{cases}x=2\\x^2-3x+2m-1=0\left(2\right)\end{cases}}\)
Để phương trình (1) có 3 nghiệm phân biệt thì phương trình (2) có 2 nghiệm phân biệt khác 2
Điều kiện là: \(\hept{\begin{cases}\Delta>0\\4-6+2m-1\ne0\end{cases}\Leftrightarrow\hept{\begin{cases}13-8m>0\\2m\ne3\end{cases}\Leftrightarrow\frac{3}{2}\ne}m< \frac{13}{8}}\)
b) Ta có 3 nghiệm của phương trình (1) là x1=2;x2;x3 trong đó x2;x3 là 2 nghiệm của phương trình (2)
Khi đó \(x_1^2+x_2^2+x_3^2=11\Leftrightarrow4+\left(x_2+x_3\right)^2-2x_2x_3=11\Leftrightarrow\left(x_2+x_3\right)^2-2x_2x_3=7\left(3\right)\)
Áp dụng định lý Vi-ét đối với phương trình (2) ta có : \(\hept{\begin{cases}x_2+x_3=3\\x_2x_3=2m-1\end{cases}}\)
Vậy (3) \(\Leftrightarrow9-2\left(2m-1\right)=7\Leftrightarrow m=1\left(TM\text{Đ}K\right)\)
Vậy m=1

(IMO 2016 mà đưa vô đây chi?)
Dễ thấy nếu xoá ít hơn 2016 nhân tử thì không được, vì khi đó ở hai vế sẽ có nhân tử chung.
Ta sẽ CM có thể xoá đúng 2016 nhân tử, bằng cách:
\(\left(x-1\right)\left(x-4\right)\left(x-5\right)\left(x-8\right)...=\left(x-2\right)\left(x-3\right)\left(x-6\right)\left(x-7\right)...\)
Tự CM pt này vô nghiệm nha bạn.
\(x=3+2\sqrt{2}\)
\(x-3-2\sqrt{2}=0\)
\(x-\left(3+2\sqrt{2}\right)=0\) Vậy nhân tử của \(x=3+2\sqrt{2}\) là \(x-\left(3+2\sqrt{2}\right)\)