K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
6 tháng 7 2017
Ta có BC < BD mà C, D nằm cùng phía so với B ⇒ C nằm giữa B và D.
HH
20 tháng 2 2018
(Bạn tự vẽ hình giùm)
a/ Ta có \(\widehat{ABC}=\widehat{ACB}\)(\(\Delta ABC\)cân tại A)
=> 180o - \(\widehat{ABC}\)= 180o - \(\widehat{ACB}\)
=> \(\widehat{ABD}=\widehat{ACE}\)
\(\Delta ABD\)và \(\Delta ACE\)có: AB = AC (\(\Delta ABC\)cân tại A)
\(\widehat{ABD}=\widehat{ACE}\)(cmt)
BD = CE (gt)
=> \(\Delta ABD\)= \(\Delta ACE\)(c - g - c) => AD = AE (hai cạnh tương ứng) => \(\Delta ADE\)cân tại A (đpcm)
b/ Mình xin chỉnh lại đề: Kẻ \(BH\perp AD\); \(CK\perp AE\). Chứng minh rằng: AH = AK.
\(\Delta BHD\)vuông và \(\Delta CKE\)vuông có: BD = CE (gt)
\(\widehat{D}=\widehat{E}\)(\(\Delta ADE\)cân tại A)
=> \(\Delta BHD\)vuông = \(\Delta CKE\)vuông (cạnh huyền - góc nhọn) => HD = KE (hai cạnh tương ứng)
và AD = AE (\(\Delta ADE\)cân tại A)
=> AD - HD = AE - KE
=> AH = AK (đpcm)
HN
21 tháng 5 2017
A B C D E I F
Kẻ ID \(\perp\) AB, IE \(\perp\) BC, IF \(\perp\) AC
Xét hai tam giác vuông IBD và IBE có:
IB: cạnh chung
\(\widehat{DBI}=\widehat{EBI}\) (gt)
Vậy: \(\Delta IBD=\Delta IBE\left(ch-gn\right)\)
\(\Rightarrow\) ID = IE (hai cạnh tương ứng) (1)
Xét hai tam giác vuông ICF và ICE có:
IC: cạnh chung
\(\widehat{FCI}=\widehat{ECI}\) (gt)
Vậy: \(\Delta ICF=\Delta ICE\left(ch-gn\right)\)
\(\Rightarrow\) IF = IE (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông AID và AIF có:
AI: cạnh chung
ID = IF (cmt)
Vậy: \(\Delta AID=\Delta AIF\left(ch-cgv\right)\)
\(\Rightarrow\widehat{IAD}=\widehat{IAF}\) (hai góc tương ứng)
Do đó: AI là tia phân giác của \(\widehat{A}\).
C
0
Y
3
MT
22 tháng 6 2015
http://olm.vn/hoi-dap/question/107283.html
bạn vào đây mjk giải ở đây
MT
22 tháng 6 2015
x t y x' t' y'
xét các tia x'o;ox và y'o;oy, có hai góc đối đỉnh là xoy và x'oy'
gọi ot và ot' là hai tia phân giác tương ứng
Thấy: góc xoy = góc x'oy'
=> góc yot = góc y'ot'
ta có: góc xoy + góc xoy' = góc toy' + góc yot = 1800
<=> góc toy' + góc y'ot' = góc tot' = 1800
=> ot và ot' là hài tia đối nhau
CM
19 tháng 11 2018
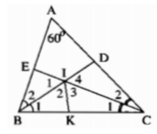
Trong ΔABC, ta có:
∠A +∠B +∠C = 180o (tổng ba góc trong tam giác)
⇒∠B +∠C = 180 - ∠A = 180 - 60 = 120o
+) Vì BD là tia phân giác của ABC nên: ∠(B1 ) = ∠(B2) = 1/2 ∠B
Vì CE là tia phân giác của góc ACB nên: ∠(C1 ) = ∠(C2) = 1/2 ∠ C
Do đó:
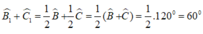
Trong ΔBIC, ta có:
∠(BIC) = 180o(∠(B1 ) + ∠(C1) = 180o - 60o = 120o
Kẻ tia phân giác ∠(BIC) cắt cạnh BC tại K
Suy ra: ∠(I2 ) = ∠(I3 ) = 1/2 ∠(BIC) = 60o
Ta có: ∠(I1 ) + ∠(BIC) = 180o (hai góc kề bù)
⇒ ∠(I1 ) = 180o-∠(BIC) = 180o - 120o = 60o
∠(I4 ) = ∠(I1) = 60o(vì hai góc đối đỉnh)
Xét ΔBIE và ΔBIK, ta có
∠(B2) = ∠(B1) (vì BD là tia phân giác của góc ABC)
BI cạnhchung
∠(I1) = ∠(I2) = 60o
Suy ra: ΔBIE = ΔBIK(g.c.g)
IK = IE (hai cạnh tương ứng) (1)
Xét ΔCIK và ΔCID, ta có
∠(C1) = ∠(C2) ( vì CE là tia phân giác của góc ACB).
CI cạnh chung
∠(I3) = ∠(I4) = 60o
Suy ra: ΔCIK = ΔCID(g.c.g)
IK = ID (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: IE = ID