Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bài 2:
a: Xét ΔOHA vuông tại A và ΔOHB vuông tại B có
OH chung
\(\widehat{AOH}=\widehat{BOH}\)
Do đó: ΔOHA=ΔOHB
Suy ra: HA=HB
hay ΔHAB cân tại H
b: Xét ΔOAB có
OH là đường cao
AD là đường cao
OH cắt AD tại C
Do đó: C là trực tâm của ΔOAB
Suy ra: BC\(\perp\)Ox
c: \(\widehat{HOA}=\dfrac{60^0}{2}=30^0\)
Xét ΔOHA vuông tại A có
\(\cos HOA=\dfrac{OA}{OH}\)
\(\Leftrightarrow OA=\dfrac{\sqrt{3}}{2}\cdot4=2\sqrt{3}\left(cm\right)\)
Đáp án B
Gọi hình bình hành là ABCD và
d:x+ y-1 = 0, ∆: 3x – y+ 5= 0 .
Không làm mất tính tổng quát giả sử
Ta có : 
. Vì I(3;3) là tâm hình bình hành nên C(7;4) ; 
=> Đường thẳng ACcó pt là: x- 4y + 9= 0.
Do 
=> Đường thẳng BC đi qua điểm C và có vtpt 
có pt là: 3x – y- 17= 0.
Khi đó :
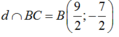
Ta có:
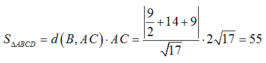
Đáp án B
Phương trình chính tắc của elip có dạng:
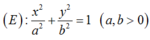
Do một cạnh của hình chữ nhật cơ sở thuộc đường thẳng x-2 = 0 nên có a= 2.
Mặt khác độ dài đường chéo là 6 nên a2 + b2= 62 nên b2= 36- 4= 32
=> 
Vậy (E) cần tìm là:
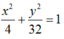
Gọi A,B lần lượt là giao của (d) với trục Ox và Oy
\(\Leftrightarrow A\left(\dfrac{1-m}{m};0\right);B\left(0;m-1\right)\)
\(\Leftrightarrow OA=\left|\dfrac{m-1}{m}\right|;OB=\left|m-1\right|\)
=>\(OA\cdot OB=2\cdot2=4\)
=>|m-1|^2/|m|=4
=>m^2-2m+1=4|m|
TH1: m>=0
Pt sẽ là m^2-2m+1=4m
=>m^2-6m+1=0
hay \(m=3\pm2\sqrt{2}\)
TH2: m<0
Pt sẽ là m^2-2m+1=-4m
=>m^2+2m+1=0
=>m=-1
1: Xét tứ giác AEHF có \(\widehat{AEH}+\widehat{AFH}=180^0\)
nên AEHF là tứ giác nội tiếp
2: Xét ΔCDA vuông tại D và ΔCEB vuông tại E có
\(\widehat{DCA}\) chung
Do đó: ΔCDA\(\sim\)ΔCEB
Suy ra: CD/CE=CA/CB
hay \(CD\cdot CB=CA\cdot CE\)
Chắc điểm D kia là C?
\(\overrightarrow{AB}=\left(4;14\right)=2\left(2;7\right)\)
\(\Rightarrow\) Đường thẳng AB nhận \(\left(7;-2\right)\) là 1 vtpt
Phương trình AB:
\(7\left(x-2\right)-2\left(y-1\right)=0\Leftrightarrow7x-2y-12=0\)
\(\overrightarrow{CB}=\left(2;6\right)=2\left(1;3\right)\Rightarrow\) đường cao AH vuông góc BC nên nhận (1;3) là 1 vtpt
Phương trình AH:
\(1\left(x-2\right)+3\left(y-1\right)=0\Leftrightarrow x+3y-5=0\)
\(\overrightarrow{AC}=\left(2;8\right)=2\left(1;4\right)\Rightarrow\) đường thẳng AC nhận (4;-1) là 1 vtpt
Phương trình AC: \(4\left(x-2\right)-1\left(y-1\right)=0\Leftrightarrow4x-y-7=0\)
Gọi \(M\left(x;y\right)\) là điểm bất kì thuộc phân giác góc A
\(\Rightarrow d\left(M;AB\right)=d\left(M;AC\right)\)
\(\Rightarrow\dfrac{\left|7x-2y-12\right|}{\sqrt{7^2+\left(-2\right)^2}}=\dfrac{\left|4x-y-7\right|}{\sqrt{4^2+\left(-1\right)^2}}\)
\(\Leftrightarrow\sqrt{17}\left|7x-2y-12\right|=\sqrt{53}\left|4x-y-7\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}7\sqrt{17}x-2\sqrt{17}y-12\sqrt{17}=4\sqrt{53}x-\sqrt{53}y-7\sqrt{53}\\7\sqrt{17}x-2\sqrt{17}y-12\sqrt{17}=-4\sqrt{53}x+\sqrt{53}y+7\sqrt{53}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(7\sqrt{17}-4\sqrt{53}\right)x+\left(\sqrt{53}-2\sqrt{17}\right)y-12\sqrt{17}+7\sqrt{53}=0\\\left(7\sqrt{17}+4\sqrt{53}\right)x-\left(\sqrt{53}+2\sqrt{17}\right)y-12\sqrt{17}-7\sqrt{53}=0\end{matrix}\right.\)
Đây là pt 2 phân giác trong và ngoài của góc A