Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tập xác định : D = R { 1 }.
> 0, ∀x
1.
Hàm số đồng biến trên các khoảng : (-∞ ; 1), (1 ; +∞).
b) Tập xác định : D = R { 1 }.
< 0, ∀x
1.
Hàm số nghịch biến trên các khoảng : (-∞ ; 1), (1 ; +∞).
c) Tập xác định : D = (-∞ ; -4] ∪ [5 ; +∞).
∀x ∈ (-∞ ; -4] ∪ [5 ; +∞).
Với x ∈ (-∞ ; -4) thì y’ < 0; với x ∈ (5 ; +∞) thì y’ > 0. Vậy hàm số nghịch biến trên khoảng (-∞ ; -4) và đồng biến trên khoảng (5 ; +∞).
d) Tập xác định : D = R { -3 ; 3 }.
< 0, ∀x
±3.
Hàm số nghịch biến trên các khoảng : (-∞ ; -3), (-3 ; 3), (3 ; +∞).

a) Tập xác định : R\ {1}; y′=−4(x−1)2<0,∀x≠1y′=−4(x−1)2<0,∀x≠1 ;
Tiệm cận đứng : x = 1 . Tiệm cận ngang : y = 1.
Bảng biến thiên :
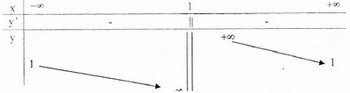
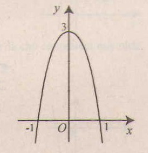
Đồ thị như hình bên. 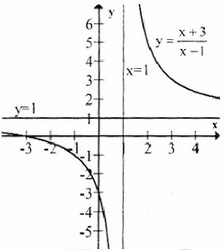
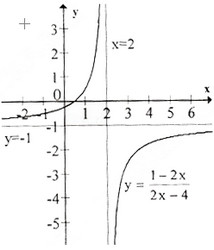
b) Tập xác định : R \{2}; y′=6(2x−4)2>0,∀x≠2y′=6(2x−4)2>0,∀x≠2
Tiệm cận đứng : x = 2 . Tiệm cận ngang : y = -1.
Bảng biến thiên :
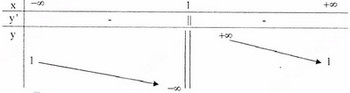
Đồ thị như hình bên.
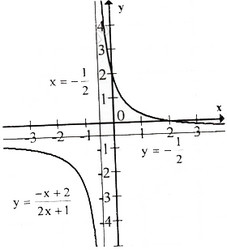
c) Tập xác định : R∖{−12}R∖{−12}; y′=−5(2x+1)2<0,∀x≠−12y′=−5(2x+1)2<0,∀x≠−12
Tiệm cận đứng : x=−12x=−12 . Tiệm cận ngang : y=−12y=−12.
Bảng biến thiên :
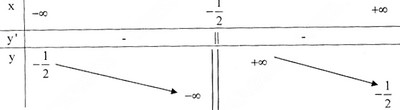
Đồ thị như hình bên.

- Điều kiện đồng biến, nghịch biến của hàm số:
Cho hàm số y = f(x) có đạo hàm trên khoảng K.
+ f(x) đồng biến (tăng) trên K nếu f’(x) > 0 với ∀ x ∈ K.
+ f(x) nghịch biến (giảm) trên K nếu f’(x) < 0 với ∀ x ∈ K.
- Xét hàm số
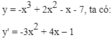
+ Hàm số đồng biến
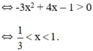
+ Hàm số nghịch biến
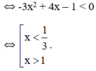
Vậy hàm số đồng biến trên 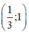
nghịch biến trên các khoảng 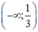 và (1; +∞)
và (1; +∞)
- Xét hàm số 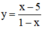
Ta có: D = R \ {1}
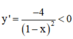 ∀ x ∈ D.
∀ x ∈ D.
⇒ Hàm số nghịch biến trên từng khoảng (-∞; 1) và (1; +∞).

a) Tập xác định : R ; y' =-4x3 + 16x = -4x(x2 - 4);
y' = 0 ⇔ x = 0, x = ±2 .
Bảng biến thiên :
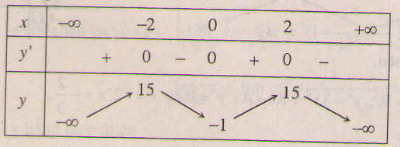
Đồ thị như hình bên.
b) Tập xác định : R ; y' =4x3 - 4x = 4x(x2 - 1);
y' = 0 ⇔ x = 0, x = ±1 .
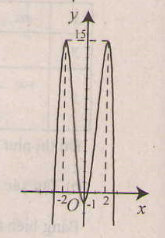
Bảng biến thiên :
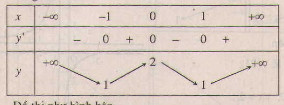
Đồ thị như hình bên.
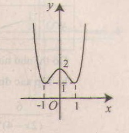
c) Tập xác định : R ; y' =2x3 + 2x = 2x(x2 + 1); y' = 0 ⇔ x = 0.
Bảng biến thiên :
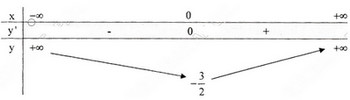
Đồ thị như hình bên.
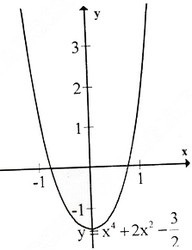
d) Tập xác định : R ; y' = -4x - 4x3 = -4x(1 + x2); y' = 0 ⇔ x = 0.
Bảng biến thiên :
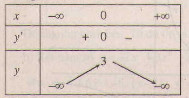
Đồ thị như hình bên.
 .
.

a) Vì ![]() ( hoặc
( hoặc ![]() ) nên đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.
) nên đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.
Vì ![]() ( hoặc
( hoặc ![]() ) nên đường thẳng y = -1 là tiệm cận ngang của đồ thị hàm số.
) nên đường thẳng y = -1 là tiệm cận ngang của đồ thị hàm số.
b) Tiệm cận đứng : x = -1 ; tiệm cận ngang : y = -1.
c) Tiệm cận đứng : ![]() ; tiệm cận ngang :
; tiệm cận ngang :
d) Tiệm cận đứng : x = 0 ; tiệm cận ngang : y = -1.
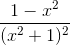 => y' = 0 ⇔ x=-1 hoặc x=1.
=> y' = 0 ⇔ x=-1 hoặc x=1.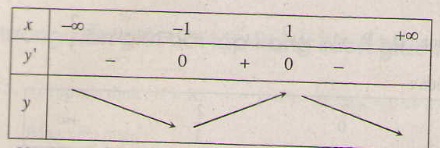
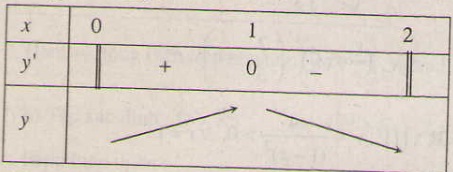


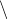 {
{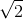 ) ∈ ∆ ⇔
) ∈ ∆ ⇔ 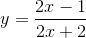 .
.
*Xét hàm số: y= -x3 + 2x2 – x – 7
Tập xác định: D = R
\(y'\left(x\right)=-3x^2+4x-1\); \(y'\left(x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{3}\end{matrix}\right.\)
y’ > 0 với và y’ < 0 với \(x \in ( - \infty ,{1 \over 3}) \cup (1, + \infty )
Vậy hàm số đồng biến trong (\(\dfrac{1}{3}\),1)(\(\dfrac{1}{3}\),1) và nghịch biến trong (−∞,13)∪(1,+∞)(−∞,13)b) Xét hàm số: \(y=\dfrac{x-5}{1-x}\).
Tập xác định: D = R{1}
\(y'=\dfrac{-4}{\left(1-x\right)^2}< 0,\forall x\in D\)
Vậy hàm số nghịch biến trong từng khoảng (-∞,1) và (1, +∞)