
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng định lí tổng bốn góc trong một tứ giác vào tứ giác HEFG, ta có:
\(\widehat H + \widehat E + \widehat F + \widehat G = {360^o}\)
\(\widehat E\)+10°+\(\widehat E\)+60°+50°=360o
2\(\widehat E\)+120°=360°
Suy ra 2\(\widehat E\)=360°−120°=240°
Khi đó \(\widehat E\)=120°
Suy ra \(\widehat H\)=\(\widehat E\)+10°=120°+10°=130°
Vậy \(\widehat H\)=130°; \(\widehat E\)= 120°

Áp dụng định lý Py-ta-go cho tam giác ABC vuông tại A ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}\)
\(\Rightarrow BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
Ta có:
\(\dfrac{AB}{DE}=\dfrac{3}{15}=\dfrac{1}{5}\)
\(\dfrac{AC}{DF}=\dfrac{4}{20}=\dfrac{1}{5}\)
\(\dfrac{BC}{EF}=\dfrac{5}{25}=\dfrac{1}{5}\)
\(\Rightarrow\dfrac{AB}{DE}=\dfrac{AC}{DF}=\dfrac{BC}{EF}=\dfrac{1}{5}\)
Xét hai tam giác ABC và DEF có:
\(\dfrac{AB}{DE}=\dfrac{AC}{DF}=\dfrac{BC}{EF}\left(=\dfrac{1}{5}\right)\)
\(\Rightarrow\Delta ABC\sim\Delta DEF\left(c.c.c\right)\)

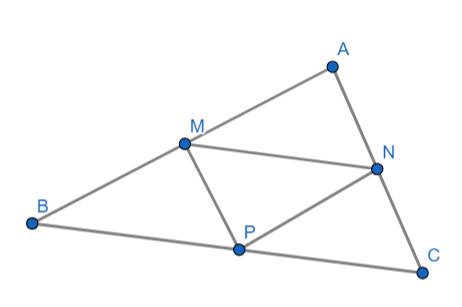
a) Ta có:
M là trung điểm của AB
N là trung điểm của AC
⇒ MN là đường trung bình của tam giác ABC
⇒ MN // BC
\(\Rightarrow\widehat{AMN}=\widehat{ABC}\) (đồng vị)
Xét hai tam giác ABC và AMN có:
\(\widehat{AMN}=\widehat{ABC}\left(cmt\right)\)
\(\widehat{BAC}\) chung
\(\Rightarrow\Delta ABC\sim\Delta AMN\left(g.g\right)\)
b) Chứng minh tương tự như câu a thì ta có:
PN cũng là đường trung bình của tam giác ABC \(\Rightarrow PN=\dfrac{1}{2}AB\)
PM cũng là đường trung bình của tam giác ABC \(\Rightarrow PM=\dfrac{1}{2}AC\)
Mà: \(NM=\dfrac{1}{2}BC\) (NM là đường trung bình ...)
Xét hai tam giác ABC và PNM có:
\(\dfrac{PN}{AB}=\dfrac{PM}{AC}=\dfrac{NM}{BC}=\dfrac{1}{2}\)
\(\Rightarrow\Delta ABC\sim\Delta PNM\left(c.c.c\right)\)

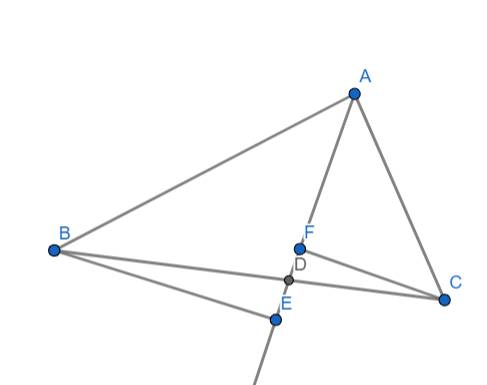
a) Ta có: E,F lần lược là hình chiếu của B,C trên AD
\(\Rightarrow\left\{{}\begin{matrix}\widehat{BEA}=90^o\\\widehat{CFA}=90^o\end{matrix}\right.\)
Xét hai tam giác ABE và ACF có:
\(\widehat{BEA}=\widehat{CFA}\left(=90^o\right)\)
\(\widehat{BAE}=\widehat{CAF}\) (do AD là phân giác của góc A)
\(\Rightarrow\Delta ABE\sim\Delta ACF\left(g.g\right)\)
b) Xét hai tam giác BDE và CDF có:
\(\widehat{BDE}=\widehat{CDF}\) (đối đỉnh)
\(\widehat{BED}=\widehat{CFD}\left(=90^o\right)\)
\(\Rightarrow\Delta BDE\sim\Delta CDF\left(g.g\right)\)
\(\Rightarrow\dfrac{BE}{CF}=\dfrac{DE}{DF}\) (1)
Mà: \(\Delta ABE\sim\Delta ACF\left(cmt\right)\)
\(\Rightarrow\dfrac{BE}{CF}=\dfrac{AE}{AF}\left(2\right)\)
Từ (1) và (2) ta có: \(\dfrac{DE}{DF}=\dfrac{AE}{AF}\Rightarrow AF\cdot DE=AE\cdot DF\)

a) Đường thẳng \(y=ax+b\) song song với đường thẳng \(y=4x-3\)
Nên có \(a=4\) đường thẳng có dạng \(y=3x+b\left(b\ne-3\right)\)
Mà \(y=3x+b\) đi qua điểm \(I\left(\dfrac{1}{2};\dfrac{3}{4}\right)\) nên ta thay \(x=\dfrac{1}{2};y=\dfrac{3}{4}\) ta có:
\(\dfrac{3}{4}=3\cdot\dfrac{1}{2}+b\)
\(\Leftrightarrow\dfrac{3}{4}=\dfrac{3}{2}+b\)
\(\Leftrightarrow b=\dfrac{3}{4}-\dfrac{3}{2}\)
\(\Leftrightarrow b=-\dfrac{3}{4}\left(tm\right)\)
Vậy: \(y=4x-\dfrac{3}{4}\)
b) Đường thẳng \(y=ax+b\) có hệ số góc \(a=3\) nên có dạng \(y=3x+b\)
Do đường thẳng cắt trục tung tại điểm có tung độ là - 4 nên ta thay \(x=0;y=-4\)
\(-4=0\cdot3+b\)
\(\Leftrightarrow b=-4\)
Vậy: \(y=3x-4\)

\(y=\left(m-3\right)+m^2\) có: \(\left\{{}\begin{matrix}a=m-3\\b=m^2\end{matrix}\right.\)
a) Để \(y=\left(m-3\right)x+m^2\) cắt \(y=3x+5\) thì:
\(a\ne a'\) hay:
\(m-3\ne3\)
\(\Leftrightarrow m\ne3+3\)
\(\Leftrightarrow m\ne6\)
b) Để \(y=\left(m-3\right)x+m^2\) song song với \(y=-2x+1\) thì
\(\left\{{}\begin{matrix}a=a'\\b\ne b'\end{matrix}\right.\) hay:
\(\left\{{}\begin{matrix}m-3=-2\\m^2\ne1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=-2+3\\m\ne\pm1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=1\\m\ne\pm1\end{matrix}\right.\) (ktm)
Vậy không có m thỏa mãn
c) Để \(y=\left(m-3\right)x+m^2\) trùng với \(y=-x+4\) thì
\(\left\{{}\begin{matrix}a=a'\\b=b'\end{matrix}\right.\) hay:
\(\left\{{}\begin{matrix}m-3=-1\\m^2=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=-1+3\\m=\pm2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=2\\m=\pm2\end{matrix}\right.\Leftrightarrow m=2\)

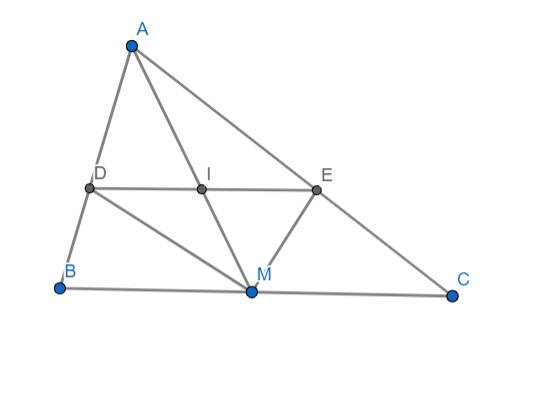
a) Ta có ME là tia phân giác của góc AMC nên:
\(\dfrac{AM}{AE}=\dfrac{MC}{CE}\Rightarrow\dfrac{AM}{MC}=\dfrac{AE}{CE}\) (1)
MD là tia phân giác của góc AMB nên:
\(\dfrac{AM}{AD}=\dfrac{BM}{BD}\Rightarrow\dfrac{AM}{BM}=\dfrac{AM}{CM}=\dfrac{AD}{BD}\) (vì M là trung điểm của BC nên BM = CM) (2)
Từ (1) và (2) ta có: \(\dfrac{AE}{CE}=\dfrac{AD}{BD}\Rightarrow DE//BC\)
b) Ta có: \(\Delta ADE\sim\Delta ABC\left(g.g\right)\) (vì có DE//BC)
\(\Rightarrow\dfrac{DE}{BC}=\dfrac{AE}{AC}\) (3)
\(\Delta AIE\sim\Delta AMC\left(g.g\right)\) (vì có IE//MC)
\(\Rightarrow\dfrac{IE}{MC}=\dfrac{AE}{AC}\) (4)
Từ (3) và (4) ta có: \(\dfrac{DE}{BC}=\dfrac{IE}{MC}\Rightarrow\dfrac{DE}{IE}=\dfrac{BC}{MC}=2\)
\(\Rightarrow DE=2IE\)
Hay I là trung điểm của DE


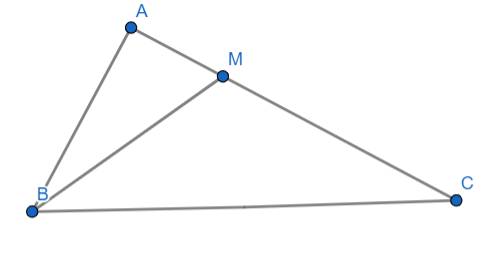
a) Áp dụng định lý Py-ta-go cho tam giác ABC vuông tại A ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}\)
\(\Rightarrow BC=\sqrt{10^2+20^2}=10\sqrt{5}\left(cm\right)\)
Áp dụng định lý Py-ta-go cho tam giác ABM vuông tại A ta có:
\(BM^2=AB^2+AM^2\)
\(\Rightarrow BM=\sqrt{AB^2+AM^2}\)
\(\Rightarrow BM=\sqrt{10^2+5^2}=5\sqrt{5}\left(cm\right)\)
b) Ta có:
\(\dfrac{AM}{AB}=\dfrac{1}{2}\)
\(\dfrac{BM}{BC}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{AM}{AB}=\dfrac{MB}{BC}=\dfrac{1}{2}\)
Xét hai tam giác ABC và AMB có:
\(\widehat{BAC}\) chung
\(\dfrac{AM}{AB}=\dfrac{MB}{BC}=\dfrac{1}{2}\)
\(\Rightarrow\Delta ABC\sim\Delta AMB\left(c.g.c\right)\)

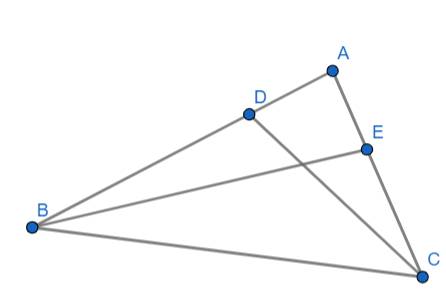
a) Xét hai tam giác ABE và ACD có:
\(\widehat{ACD}=\widehat{ABE}\left(gt\right)\)
\(\widehat{BAC}\) chung
\(\Rightarrow\Delta ABE\sim\Delta ACD\left(g.g\right)\)
b) Ta có: \(\Delta ABE\sim\Delta ACD\left(cmt\right)\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{AE}{AD}\)
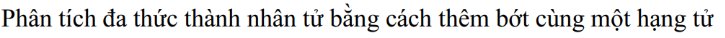
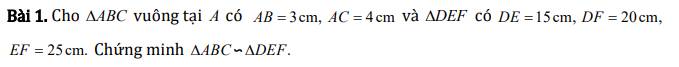

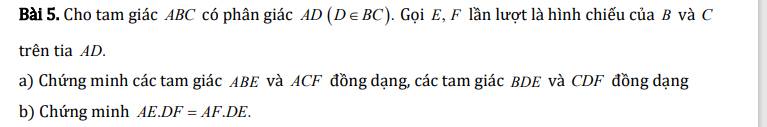
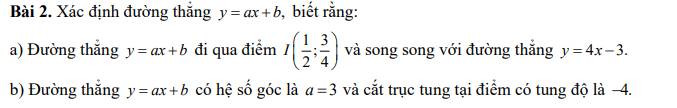


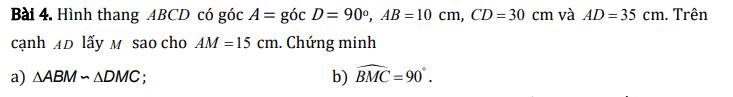
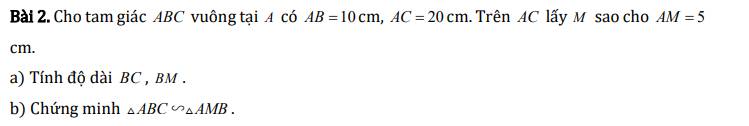
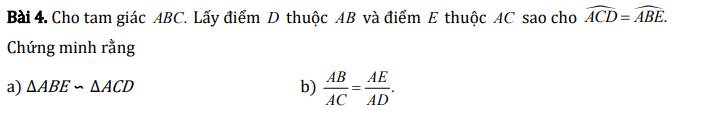
\(x^7+x^2+1\)
\(=x^7+x^6+x^5-x^6-x^5-x^4+x^4+x^3+x^2-x^3-x^2-x+x^2+x+1\)
\(=x^5\left(x^2+x+1\right)-x^4\left(x^2+x+1\right)+x^2\left(x^2+x+1\right)-x\left(x^2+x+1\right)+\left(x^2+x+1\right)\)
\(=\left(x^2+x+1\right)\left(x^5-x^4+x^2-x+1\right)\)