
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
\(\lim\frac{6n^3-2n+1}{(5n^3-n)(n^2+n-1)}=\lim \frac{6-\frac{2}{n^2}+\frac{1}{n^3}}{(5-\frac{1}{n^2})(n^2+n-1)}\)
Ta thấy:
\(\lim\frac{6-\frac{2}{n^2}+\frac{1}{n^3}}{5-\frac{1}{n^2}}=\frac{6}{5}\)
\(\lim \frac{1}{n^2+n-1}=0\)
$\Rightarrow L=0$

Bạn xem lại câu a nhé! Làm gì phải là m2
b) \(lim\left(1+n^2-\sqrt{n^4+3n+1}\right)=lim\frac{\left(n^4+2n^2+1\right)-\left(n^4+3n+1\right)}{1+n^2+\sqrt{n^4+3n+1}}\)
\(=lim\frac{2n^2+3n}{1+n^2+\sqrt{n^4+3n+1}}=lim\frac{2+\frac{3}{n}}{\frac{1}{n^2}+1+\sqrt{1+\frac{3}{n}+\frac{1}{n^2}}}=\frac{2}{2}=1\)
c) = \(lim\frac{1}{\sqrt{n+1}+\sqrt{n}}=0\)
d) = \(lim\frac{n+1}{\sqrt{n^2+n+1}+n}=lim\frac{1+\frac{1}{n}}{\sqrt{1+\frac{1}{n}+\frac{1}{n^2}}+1}=\frac{1}{2}\)

3:
\(\lim\limits_{n\rightarrow\infty}\dfrac{2-5^{n-2}}{3^n+2\cdot5^n}\)
\(=\lim\limits_{n\rightarrow\infty}\dfrac{\dfrac{2}{5^n}-\dfrac{5^{n-2}}{5^n}}{\dfrac{3^n}{5^n}+2\cdot\dfrac{5^n}{5^n}}\)
\(=\lim\limits_{n\rightarrow\infty}\dfrac{\dfrac{2}{5^n}-\dfrac{1}{25}}{\left(\dfrac{3}{5}\right)^n+2\cdot1}\)
\(=-\dfrac{1}{25}:2=-\dfrac{1}{50}\)
1:
\(=\lim\limits_{n\rightarrow\infty}\dfrac{3^n-4^n\cdot4}{3^n\cdot9+4^n}\)
\(=\lim\limits_{n\rightarrow\infty}\dfrac{\dfrac{3^n}{4^n}-4}{3^n\cdot\dfrac{9}{4^n}+1}\)
\(=-\dfrac{4}{1}=-4\)

1: \(-1< =cosx< =1\)
=>\(-3< =3\cdot cosx< =3\)
=>\(y\in\left[-3;3\right]\)
2:
TXĐ là D=R
3: \(L=\lim\limits\dfrac{-3n^3+n^2}{2n^3+5n-2}\)
\(=\lim\limits\dfrac{-3+\dfrac{1}{n}}{2+\dfrac{5}{n^2}-\dfrac{2}{n^3}}=-\dfrac{3}{2}\)
4:
\(L=lim\left(3n^2+5n-3\right)\)
\(=\lim\limits\left[n^2\left(3+\dfrac{5}{n}-\dfrac{3}{n^2}\right)\right]\)
\(=+\infty\) vì \(\left\{{}\begin{matrix}lim\left(n^2\right)=+\infty\\\lim\limits\left(3+\dfrac{5}{n}-\dfrac{3}{n^2}\right)=3>0\end{matrix}\right.\)
5:
\(\lim\limits_{n\rightarrow+\infty}n^3-2n^2+3n-4\)
\(=\lim\limits_{n\rightarrow+\infty}n^3\left(1-\dfrac{2}{n}+\dfrac{3}{n^2}-\dfrac{4}{n^3}\right)\)
\(=+\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{n\rightarrow+\infty}n^3=+\infty\\\lim\limits_{n\rightarrow+\infty}1-\dfrac{2}{n}+\dfrac{3}{n^2}-\dfrac{4}{n^3}=1>0\end{matrix}\right.\)
\(1,y=3cosx\)
\(+TXD\) \(D=R\)
Có \(-1\le cosx\le1\)
\(\Leftrightarrow-3\le3cosx\le3\)
Vậy có tập giá trị \(T=\left[-3;3\right]\)
\(2,y=cosx\)
\(TXD\) \(D=R\)
\(3,L=lim\dfrac{n^2-3n^3}{2n^3+5n-2}=lim\dfrac{\dfrac{1}{n}-3}{2+\dfrac{5}{n^2}-\dfrac{2}{n^3}}\)(chia cả tử và mẫu cho \(n^3\))
\(=\dfrac{lim\dfrac{1}{n}-lim3}{lim2+5lim\dfrac{1}{n^2}-2lim\dfrac{1}{n^3}}=\dfrac{0-3}{2+5.0-2.0}=-\dfrac{3}{2}\)
\(4,L=lim\left(3n^2+5n-3\right)\\ =lim\left(3+\dfrac{5}{n}-\dfrac{3}{n^2}\right)\\ =lim3+5lim\dfrac{1}{n}-3lim\dfrac{1}{n^2}\\ =3\)
\(5,\lim\limits_{n\rightarrow+\infty}\left(n^3-2n^2+3n-4\right)\\ =lim\left(1-\dfrac{2}{n}+\dfrac{3}{n^2}-\dfrac{4}{n^3}\right)\\ =lim1-0\\ =1\)
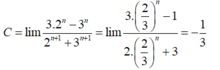
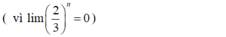
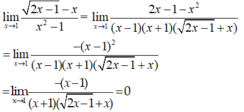
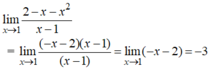
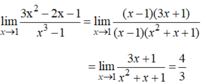
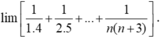
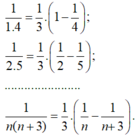
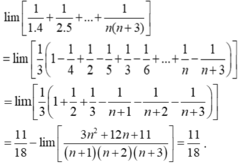
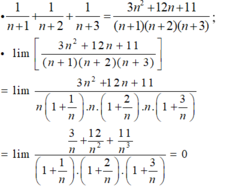
- Đặt:
- Nên: