
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

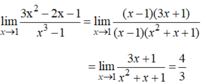

a) \(\lim\limits_{x\rightarrow-2}\dfrac{2x^2+x-6}{x^3+8}=\lim\limits_{x\rightarrow-2}\dfrac{\left(2x-3\right)\left(x+2\right)}{\left(x+2\right)\left(x^2-2x+4\right)}\\ =\lim\limits_{x\rightarrow-2}\dfrac{2x-3}{x^2-2x+4}=-\dfrac{7}{12}\).
b) \(\lim\limits_{x\rightarrow3}\dfrac{x^4-x^2-72}{x^2-2x-3}=\lim\limits_{x\rightarrow3}\dfrac{\left(x^2+8\right)\left(x+3\right)\left(x-3\right)}{\left(x-3\right)\left(x+1\right)}\\ =\lim\limits_{x\rightarrow3}\dfrac{\left(x^2+8\right)\left(x+3\right)}{x+1}=\dfrac{51}{2}\).
c) \(\lim\limits_{x\rightarrow-1}\dfrac{x^5+1}{x^3+1}=\lim\limits_{x\rightarrow-1}\dfrac{\left(x+1\right)\left(x^4-x^3+x^2-x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}\\ =\lim\limits_{x\rightarrow-1}\dfrac{x^4-x^3+x^2-x+1}{x^2-x+1}=\dfrac{5}{3}\).
d) \(\lim\limits_{x\rightarrow1}\left(\dfrac{2}{x^2-1}-\dfrac{1}{x-1}\right)=\lim\limits_{x\rightarrow1}\left(\dfrac{2}{\left(x-1\right)\left(x+1\right)}-\dfrac{x+1}{\left(x-1\right)\left(x+1\right)}\right)\\ =\lim\limits_{x\rightarrow1}\dfrac{1-x}{\left(x-1\right)\left(x+1\right)}=\lim\limits_{x\rightarrow1}\dfrac{-1}{x+1}=-\dfrac{1}{2}\).

\(lim_{x\rightarrow1}\frac{x^3+2x-3}{x^2-x}\)
\(=lim_{x\rightarrow1}\frac{\left(x-1\right)\left(x^2+x+3\right)}{x\left(x-1\right)}\)
\(=lim_{x\rightarrow1}\frac{x^2+x+3}{x}\)
\(=\frac{1^2+1+3}{1}\)
\(=5\)
\(lim_{x\rightarrow1}\frac{\sqrt{2x+2}-\sqrt{3x+1}}{x-1}\)
\(=lim_{x\rightarrow1}\frac{\left(2x+2\right)-\left(3x+1\right)}{\left(x-1\right)\left(\sqrt{2x+2}+\sqrt{3x+1}\right)}\)
\(=lim_{x\rightarrow1}\frac{2x+2-3x-1}{\left(x-1\right)\left(\sqrt{2x+2}+\sqrt{3x+1}\right)}\)
\(=lim_{x\rightarrow1}\frac{-x+1}{\left(x-1\right)\left(\sqrt{2x+2}+\sqrt{3x+1}\right)}\)
\(=lim_{x\rightarrow1}\frac{-1\left(x-1\right)}{\left(x-1\right)\left(\sqrt{2x+2}+\sqrt{3x+1}\right)}\)
\(=lim_{x\rightarrow1}\frac{-1}{\left(\sqrt{2x+2}+\sqrt{3x+1}\right)}\)
\(=\frac{-1}{\sqrt{2\cdot1+2}+\sqrt{3\cdot1+1}}\)
\(=\frac{-1}{2+2}=\frac{-1}{4}\)

1: \(\lim\limits_{x\rightarrow4}\dfrac{1-x}{\left(x-4\right)^2}=-\infty\)
vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow4}1-x=1-4=-3< 0\\\lim\limits_{x\rightarrow4}\left(x-4\right)^2=\left(4-4\right)^2=0\end{matrix}\right.\)
2: \(\lim\limits_{x\rightarrow3^+}\dfrac{2x-1}{x-3}=+\infty\)
vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow3^+}2x-1=2\cdot3-1=5>0\\\lim\limits_{x\rightarrow3^+}x-3=3-3>0\end{matrix}\right.\) và x-3>0
3: \(\lim\limits_{x\rightarrow2^+}\dfrac{-2x+1}{x+2}\)
\(=\dfrac{-2\cdot2+1}{2+2}=\dfrac{-3}{4}\)
4: \(\lim\limits_{x\rightarrow1^-}\dfrac{3x-1}{x+1}=\dfrac{3\cdot1-1}{1+1}=\dfrac{2}{2}=1\)

\(=lim_{x->0}\left(\dfrac{1+x^2-1}{x^2\left(\sqrt[3]{\left(1+x^2\right)^2}+\sqrt[3]{1+x^2}+1\right)}\right)\)
\(=lim_{x->0}1=1\)

Lời giải:
1.
\(\lim\limits_{x\to -1}\frac{x^{2019}+1}{x^2+x}=\lim\limits_{x\to -1}\frac{(x+1)(x^{2018}-x^{2017}+x^{2016}-....-x+1)}{x(x+1)}=\lim\limits_{x\to -1}\frac{x^{2018}-x^{2017}+x^{2016}-....-x+1}{x}\)
\(=\frac{(-1)^{2018}-(-1)^{2017}+(-1)^{2016}+....-(-1)+1}{-1}\)
\(=\frac{\underbrace{1+1+....+1+1}_{2019}}{-1}=\frac{2019}{-1}=-2019\)
2.
\(\lim\limits_{x\to 1}\frac{(x-1)+(x^2-1)+(x^3-1)+....+(x^n-1)}{x-1}\\ =\lim\limits_{x\to 1}\frac{(x-1)+(x-1)(x+1)+(x-1)(x^2+x+1)+....+(x-1)(x^{n-1}+x^{n-2}+...+x+1)}{x-1}\)
$\lim\limits_{x\to 1}[1+(x+1)+(x^2+x+1)+....+(x^{n-1}+x^{n-2}+...+x+1)]$
$=1+2+3+....+n=n(n+1):2$
\(\)

a: \(\lim\limits_{x\rightarrow-1^+}x+1=0\)
=>\(\lim\limits_{x\rightarrow-1^+}\dfrac{1}{x+1}=+\infty\)
b: \(\lim\limits_{x\rightarrow-\infty}1-x^2=\lim\limits_{x\rightarrow-\infty}\left[x^2\left(\dfrac{1}{x^2}-1\right)\right]\)
\(=-\infty\)
c: \(\lim\limits_{x\rightarrow3^-}\dfrac{x}{3-x}=\lim\limits_{x\rightarrow3^-}=\dfrac{-x}{x-3}\)
\(\lim\limits_{x\rightarrow3^-}x-3=0\)
\(\lim\limits_{x\rightarrow3^-}-x=3>0\)
=>\(\lim\limits_{x\rightarrow3^-}\dfrac{x}{3-x}=+\infty\)

a) Hàm số f(x) = xác định trên R\{
} và ta có x = 4 ∈ (
;+∞).
Giả sử (xn) là dãy số bất kì và xn ∈ (;+∞); xn ≠ 4 và xn → 4 khi n → +∞.
Ta có lim f(xn) = lim =
=
.
Vậy
=
.
b) Hàm số f(x) = xác định trên R.
Giả sử (xn) là dãy số bất kì và xn → +∞ khi n → +∞.
Ta có lim f(xn) = lim = lim
= -5.
Vậy
= -5.