Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\lambda = v/f = 2cm.\)
Số điểm dao động cực đại thỏa mãn:
\(-AB < d_2-d_1 < AB \Rightarrow -AB < (k+\frac{\triangle\varphi)}{2 \pi}\lambda < AB \\ \Rightarrow -10 < k\lambda < 10. \\ \Rightarrow -5 < k < 5.\\ \Rightarrow k = -4,-3,-2,-1,0,1,2,3,4.\)
Có 9 điểm dao động với biên độ cực đại.
Số điểm dao động cực tiểu thỏa mãn:
\(-AB < d_2-d_1 < AB \Rightarrow -AB < (2k+1+\frac{\triangle\varphi}{\pi})\frac{\lambda}{2} < AB \\ \Rightarrow -10 < (2k+1)\lambda/2 < 10 \\ \Rightarrow -5,5 < k < 4,5 \\ \Rightarrow k = -5,-4,-3,-2,-1,0,1,2,3,4.\)
Có 10 điểm dao động với biên độ cực tiểu.

\(\triangle \varphi = \frac{\pi}{2}.\)
Số điểm dao động vân cực đại trên đoạn thẳng nối hai nguồn là:
\(-AB\leq d_2-d_1\leq AB \Rightarrow -AB\leq (k+\frac{\triangle\varphi)}{2 \pi}\lambda\leq AB \\ \Rightarrow -32 \leq (k+ \frac{1}{4}) \lambda \leq 32 \Rightarrow -3,45 \leq k \leq 2,95 \\ \Rightarrow k = -3,-2,-1,0,1,2.\)
Có 6 vân cực đại.
Số điểm dao động vân cực tiểu trên đoạn thẳng nối hai nguồn là:
\(-AB\leq d_2-d_1\leq AB \Rightarrow -AB\leq (2k+1+\frac{\triangle\varphi}{\pi})\frac{\lambda}{2}\leq AB \\ \Rightarrow -32 \leq (2k+1+\frac{1}{2})5 \leq 32 \\ \Rightarrow -3,95 \leq k \leq 2,45. \\ \Rightarrow k = -3,-2,-1,0,1,2.\)
Có 6 vân cực tiểu.

+ M là một cực đại giao thoa, giữa M và trung trực của AB (cực đại giao thoa k = 0) có 3 dãy cực tiểu khác → M là cực đại ứng với k = 3.
+ Ta có 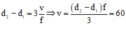 cm/s.
cm/s.
Chọn D

M A B
Giữa M và đường trung trực của AB có hai đường cực đại khác tức là M nằm ở đường cực đại thứ k = 3. (Vì đường trung trực của AB với AB cùng pha là cực đại với k = 0)
=> \(AM - BM = 3 \lambda\)
=> \(20 - 15.5 = 3 \lambda \)
=>\(3 \frac{v}{f} = 4,5cm\)
=>\(f = \frac{3v}{4,5} = 20Hz.\)
Chọn đáp án. A

Hai nguồn dao động ngược pha thì tại M dao động cực đại \(\Rightarrow d_2-d_1=(k+0,5)\lambda\)
Giữa M và trung trực AB có duy nhất 1 cực đại \(\Rightarrow k =1\)
\(\Rightarrow d_2-d_1=1,5\lambda\)
\(\Rightarrow \lambda=4/3(cm)\)
\(\Rightarrow v = \lambda.f=\dfrac{56}{3}(cm/s)\)


\(\lambda = v/f = 5cm.\)
\(\triangle \varphi = \frac{\pi}{2}.\)
Số cực đại trên đoạn AB thỏa mãn:
\(-AB < d_2-d_1 < AB \Rightarrow -AB < (k+\frac{\triangle\varphi)}{2 \pi}\lambda < AB \\ \Rightarrow -12 < (k+\frac{1}{4})\lambda < 12. \\ \Rightarrow -2,65 < k < 2,15 \\ \Rightarrow k = -2,-1,0,1,2.\)
Có 5 cực đại.
Số cực tiểu trên đoạn AB thỏa mãn:
\(-AB < d_2-d_1 < AB \Rightarrow -AB < (2k+1+\frac{\triangle\varphi}{\pi})\frac{\lambda}{2} < AB \\ \Rightarrow -12 < (2k +1 + 1/2)\lambda/2 < 12 \\ \Rightarrow -3,15 < k < 1,65 \\ \Rightarrow k = -3,-2,-1,0,1.\)
Có 5 cực tiểu.