Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do các vectơ đều nằm trên đường thẳng AB nên các vectơ này đều cùng phương với nhau.
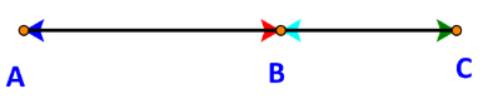
Dễ thấy:
Các vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {BC} \) cùng hướng (từ trái sang phải.)
Các vectơ \(\overrightarrow {BA} ,\overrightarrow {CA} ,\overrightarrow {CB} \) cùng hướng (từ phải sang trái.)
Do đó, các cặp vectơ cùng hướng là:
\(\overrightarrow {AB} \) và \(\overrightarrow {AC} \); \(\overrightarrow {AC} \) và \(\overrightarrow {BC} \); \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \); \(\overrightarrow {BA} \) và \(\overrightarrow {CA} \); \(\overrightarrow {BA} \) và \(\overrightarrow {CB} \);\(\overrightarrow {BA} \) và \(\overrightarrow {CB} \).
Các cặp vectơ ngược hướng là:
\(\overrightarrow {AB} \) và \(\overrightarrow {BA} \); \(\overrightarrow {AB} \) và \(\overrightarrow {CA} \); \(\overrightarrow {AB} \) và \(\overrightarrow {CB} \);
\(\overrightarrow {AC} \) và \(\overrightarrow {BA} \); \(\overrightarrow {AC} \) và \(\overrightarrow {CA} \); \(\overrightarrow {AC} \) và \(\overrightarrow {CB} \);
\(\overrightarrow {BC} \) và \(\overrightarrow {BA} \); \(\overrightarrow {BC} \) và \(\overrightarrow {CA} \); \(\overrightarrow {BC} \) và \(\overrightarrow {CB} \);

Hai vectơ \(\overrightarrow a \) và \(\overrightarrow {AB} \) cùng hướng: có giá song song và cùng hướng với nhau.
Hai vectơ \(\overrightarrow a \) và \(\overrightarrow x \) ngược hướng: có giá song song và ngược hướng với nhau.
Vectơ \(\overrightarrow z \) có giá song song với giá của vectơ \(\overrightarrow a \), ngược hướng với vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow z \) ngược hướng với nhau.
Vectơ \(\overrightarrow y \) có giá song song với giá của vectơ \(\overrightarrow a \), cùng hướng với vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow y \) cùng hướng với nhau.
Vectơ \(\overrightarrow b \) có giá không song song với giá của vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) không cùng phương với nhuau. Do vậy không xét chúng cùng hướng hay ngược hướng với nhau.

Gọi \(M,N\) là vị trí của hai vật thể sau thời gian t.
Khi đó \(\overrightarrow {AM} = t.\overrightarrow {{v_A}} = (t;2t);\overrightarrow {BN} = t.\overrightarrow {{v_B}} = (t; - 4t)\)
\( \Rightarrow \)Sau thời gian t, vị trí của hai vật thể là \(M(t + 1;2t + 1),N(t - 1; - 4t + 21)\)
Nếu hai vật thể gặp nhau thì M phải trùng N với t nào đó
\(\begin{array}{l} \Leftrightarrow (t + 1;2t + 1) = (t - 1; - 4t + 21)\\ \Leftrightarrow \left\{ \begin{array}{l}t + 1 = t - 1\\2t + 1 = - 4t + 21\end{array} \right.\end{array}\)
\( \Leftrightarrow \left\{ \begin{array}{l}1 = - 1\\2t + 1 = - 4t + 21\end{array} \right.\)(Vô lí)
Vậy hai vật thể không gặp nhau.

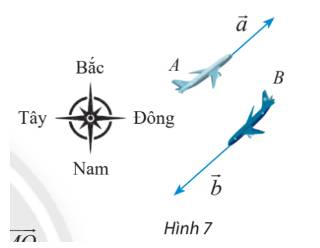
Vecto \(\overrightarrow a ,\;\overrightarrow b \) là vecto vận tốc của máy bay A và máy bay b.
Do đó \(\left| {\overrightarrow a } \right|,\;\left| {\overrightarrow b } \right|\) lần lượt là độ lớn của vecto vận tốc tương ứng.
Ta có: \(\left| {\overrightarrow a } \right| = 600,\;\left| {\overrightarrow b } \right| = 800\)
\( \Rightarrow \frac{{\left| {\overrightarrow b } \right|}}{{\left| {\overrightarrow a } \right|}} = \frac{{800}}{{600}} = \frac{4}{3}\)
Hai hướng Đông Bắc và Tây Nam là ngược nhau, do đó \(\overrightarrow b = - \frac{4}{3}\overrightarrow a \)

Gọi vận tốc dòng nước = vận tốc bè trôi = a km/h (a>0). Gọi vận tộc ca nô là x km/h (x>a); => vận tốc xuôi dong là x+a, còn ngược dòng là x-a. Do Ca nô xuôi dòng 144 km thì quay trở về A ngay , cả đi lẫn về hết 21giờ nên ta có phương trình 144/(x+a) + 144/(x-a) = 21 (1) và 144/(x+a) + (144-36)/(x-a) = 36/a <=> 144/(x+a) + 108/(x-a) = 36/a. Quy đồng rồi chuyển vế ta tìm được x=7a, thay x=7a vào (1) ta được 144/8a + 144/6a = 21 <=> 42/a = 21 <=> a=2 => x=14 (thoả mãn ĐK x>a>0). Vậy vận tốc canô là 14km/h còn vận tốc dòng nước là 2km/h. Mình nghĩ nếu bỏ phương trình (1) đi chắc cũng không sao
vậy còn cái này sao ???????

a) Ta có:
Giá của vectơ \(\overrightarrow {\rm{w}} \) trùng với giá của \(\overrightarrow x \)
Giá của vectơ \(\overrightarrow y \), \(\overrightarrow z \)song song với giá của \(\overrightarrow x \)
Suy ra các vectơ cùng phương với vectơ \(\overrightarrow x \) là \(\overrightarrow {\rm{w}} \), \(\overrightarrow y \)và \(\overrightarrow z \)
b) Ta có:
Vectơ \(\overrightarrow b \) có giá song song với vectơ \(\overrightarrow a \)và có cùng hướng từ trên xuống với vectơ \(\overrightarrow a \)nên vectơ \(\overrightarrow b \) cùng hướng với vectơ \(\overrightarrow a \)
c) Ta có:
Vectơ \(\overrightarrow v \) có giá song song với vectơ \(\overrightarrow u \)và ngược hướng từ dưới lên trên so với vectơ \(\overrightarrow u \)nên vectơ \(\overrightarrow v \) ngược hướng với vectơ \(\overrightarrow u \)

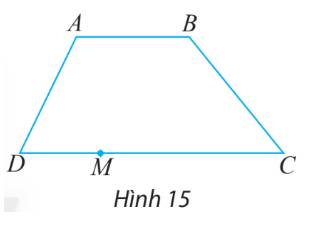
a) ABCD là hình thang nên AB//CD
Các vectơ cùng hướng với vectơ \(\overrightarrow {AB} \) là các vectơ có hướng từ trái qua phải nên đó là: \(\overrightarrow {DC} ,\overrightarrow {DM} ,\overrightarrow {MC} \)
b) \(\overrightarrow {DM} \)có hướng từ trái sang phải nên các vectơ ngược hướng với vectơ \(\overrightarrow {DM} \)là \(\overrightarrow {BA} ,\overrightarrow {MD} ,\overrightarrow {CM} ,\overrightarrow {CD} \)

A B C D O M N
a)
Các véc tơ cùng phương với \(\overrightarrow{AB}\) là:
\(\overrightarrow{MO};\overrightarrow{OM};\overrightarrow{MN};\overrightarrow{NM};\overrightarrow{NO};\overrightarrow{ON};\overrightarrow{DC};\overrightarrow{CD};\overrightarrow{BA};\overrightarrow{AB}\).
Hai véc tơ cùng hướng với \(\overrightarrow{AB}\) là:
\(\overrightarrow{MO};\overrightarrow{ON}\).
Hai véc tơ ngược hướng với \(\overrightarrow{AB}\) là:
\(\overrightarrow{OM};\overrightarrow{ON}\).
b) Một véc tơ bằng véc tơ \(\overrightarrow{MO}\) là: \(\overrightarrow{ON}\).
Một véc tơ bằng véc tơ \(\overrightarrow{OB}\) là: \(\overrightarrow{DO}\).

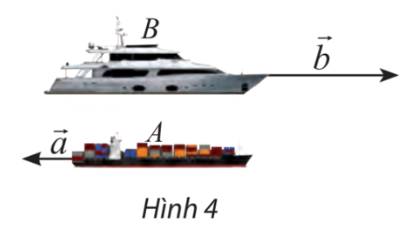
Ta thấy hai hướng đông và tây là ngược nhau và tỉ số độ dài \(\frac{{\left| {\overrightarrow b } \right|}}{{\left| {\overrightarrow a } \right|}} = \frac{{50}}{{20}} = \frac{5}{2}\)
\( \Rightarrow \overrightarrow b = - \frac{5}{2}\overrightarrow a \)


Tham khảo:
Gọi \(\overrightarrow a ,\overrightarrow b \) lần lượt là vectơ vận tốc riêng của ca nô A và B (cùng độ lớn).
Vì ca no A chạy xuôi dòng nên ngoài vận tốc riêng của ca nô, ca nô A còn được đẩy đi bởi vận tốc của dòng nước. Do đó vectơ vận tốc thực của cano A cùng hướng với vectơ \(\overrightarrow a \) và có độ lớn bằng tổng của vận tốc riêng và vận tốc dòng nước, là 18 km/h.
Ngược lại, ca nô đi ngược dòng nên bị cản lại một phần bởi dòng nước. Vì vận tốc của dòng nước nhỏ hơn vận tốc riêng của cano B nên vectơ vận tốc thực của cano B cùng hướng với vectơ \(\overrightarrow b \) và có độ lớn bằng hiệu giữa vận tốc riêng và vận tốc dòng nước, là 12 km/h.
Ta biểu diễn vận tốc thực của ca nô A và ca nô B như sau:
b) Dễ thấy:
Các vectơ \(\overrightarrow v ,\overrightarrow {{v_A}} ,\overrightarrow {{v_B}} \) đều có giá song song nên chúng cùng phương với nhau.
Ca nô A đi xuôi dòng nên vectơ vận tốc thực của ca nô A cùng hướng với vectơ vận tốc dòng nước.
Hay \(\overrightarrow v \) và \(\overrightarrow {{v_A}} \) cùng hướng.
Ca nô A đi ngược dòng nên vectơ vận tốc thực của ca nô B ngược hướng với vectơ vận tốc dòng nước.
Hay \(\overrightarrow v \) và \(\overrightarrow {{v_B}} \) ngược hướng.
Chú ý khi giải
Vận tốc riêng của cano là vận tốc của cano khi dòng nước đứng im.
Vận tốc thực của cano là vận tốc của cano khi kết hợp với dòng nước (đang chảy)