Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ So sánh NH và PH
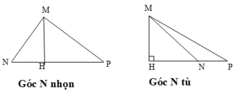
MH là đường cao của ΔMNP ⇒ H là hình chiếu của M trên đường thẳng NP.
⇒ NH là hình chiếu của đường xiên NM trên đường thẳng NP
PH là hình chiếu của đường xiên MP trên đường thẳng NP.
Mà NM < PM ⇒ NH < PH (đường xiên nào lớn hơn thì hình chiếu lớn hơn).
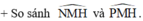
• TH1: Xét ΔMNP có góc N nhọn
⇒ góc P nhọn (vì MN < MP nên 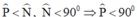 ).
).
⇒ H nằm giữa N và P.
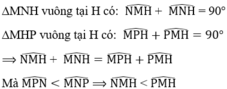
• TH2: Xét ΔMNP có góc N tù
suy ra H nằm ngoài cạnh NP.
(vì giả sử H nằm giữa N và P thì ΔMNH có 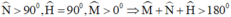 ).
).
Lại có HN < HP nên N nằm giữa H và P
⇒ Tia MN ở giữa hai tia MH và MP ⇒ 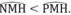

Bạn tự vẽ hình nhé !
a) Ta có MH < MN ( quan hệ góc và cạnh đối diện )
ta lại có : Góc N là góc tù
=> MN < MP ( quan hệ giữa góc và cạnh đối diện)
b) Ta có MH < MN < MP
=> HN < NP ( quan hệ đường xiên hình chiếu )
=> góc NMH < góc PMN ( quan hệ cạnh với góc đối diện )


Ta có: AB < AC (gt)
Suy ra: HB < HC (đường xiên lớn hơn thì hình chiếu lớn hơn)
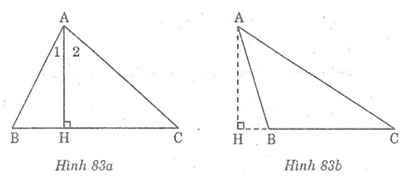
* Trường hợp góc B nhọn
Trong Δ ABC, ta có: AB < AC
Suy ra: góc B > góc C(đối diện với cạnh lớn hơn là góc lớn hơn)
Trong Δ AHB, ta có góc AHB = \(90^0\)
Suy ra: góc B + góc HAB = \(90^0\) (tính chất tam giác vuông) (1)
Trong Δ AHC, ta có góc AHC = \(90^0\)
Suy ra: góc C + góc HAC = \(90^0\) (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: góc B + góc HAB) = góc C + góc HAC
Mà góc B > góc C nên góc HAB < góc HAC
* Trường hợp Btù
Vì điểm B nằm giữa H và C nên góc HAC = góc HAB + góc BAC
Vậy góc HAB < góc HAC.
(Giải thích ở phần (**): nếu tổng của hai cặp số cùng bằng nhau (bằng 9090o chẳng hạn) thì số nào cộng với số lớn hơn thì nhỏ hơn số kia. Tức là:
a + b = 90o
c + d = 90o
mà b > d thì suy ra a < c)
Lời giải