
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a, 7+4+1=12 => Để số chia hết cho 9 thì * = 18 - 12= 6
b, 5+2+2=9 => Để số chia hết cho 3 thì *=3 hoặc *=6 hoặc *=9 hoặc *=0
c, * ở hàng đơn vị chia hết cho 2 và 5 => * hàng đơn vị: 0
1+8+2+0 =11. Để số chia hết cho 3 và 9 => * ở hàng nghìn là: 18 - 11 = 7

\(\left(\frac{x}{2}-\frac{1}{3}\right):\frac{1}{2}=\left(\frac{1}{4}-\frac{3}{2}\right):\left(1-\frac{5}{4}\right)\)
\(\left(\frac{3x-2}{6}\right):\frac{1}{2}=\left(-\frac{5}{4}\right):\left(-\frac{1}{4}\right)\)
\(\left(\frac{3x-2}{6}\right):\frac{1}{2}=5\)
\(\left(\frac{3x-2}{6}\right)=\frac{5}{2}\)
Áp dụng công thức \(\frac{a}{b}=\frac{c}{d}\Rightarrow ad=bc\) ta đc:
\(\Rightarrow2\left(3x-2\right)=30\)
\(\Rightarrow\left(3x-2\right)=15\)
\(\Rightarrow3x=17\)
\(\Rightarrow x=\frac{17}{3}\)
\(\left(\frac{x}{2}-\frac{1}{3}\right):\frac{1}{2}=\left(\frac{1}{4}-\frac{3}{2}\right):\left(\frac{1-5}{4}\right)\)
\(\left(\frac{x}{2}-\frac{1}{3}\right):\frac{1}{2}=\left(\frac{1}{4}-\frac{6}{4}\right):1\)
\(\left(\frac{x}{2}-\frac{1}{3}\right):\frac{1}{2}=-\frac{5}{4}:1\)
\(\left(\frac{x}{2}-\frac{1}{3}\right):\frac{1}{2}=-\frac{5}{4}\)
\(\frac{x}{2}-\frac{1}{3}=-\frac{5}{4}\times\frac{1}{2}\)
\(\frac{x}{2}-\frac{1}{3}=-\frac{5}{8}\)
\(\frac{x}{2}=-\frac{5}{8}+\frac{1}{3}\)
\(\frac{x}{2}=-\frac{7}{24}\)
\(x\times24=-14\)
\(x=-\frac{7}{12}\)

\(a,\Rightarrow20\cdot2^x=160+1-1\\ \Rightarrow2^x=160:20=8=2^3\\ \Rightarrow x=3\\ b,\Rightarrow\left(4-x:2\right)^3=2\left(8-5\right)+1+1\\ \Rightarrow\left(4-x:2\right)^3=6+2=8=2^3\\ \Rightarrow4-x:2=2\\ \Rightarrow x:2=2\Rightarrow x=4\\ c,n\left(n+2017\right)\)
Với n chẵn thì \(n=2k\left(k\in N\right)\Rightarrow n\left(n+2017\right)=2k\left(n+2017\right)⋮2\)
Với n lẻ thì \(n=2k+1\left(k\in N\right)\Rightarrow n\left(n+2017\right)=n\left(2k+2018\right)=2n\left(k+1009\right)⋮2\)
Vậy \(n\left(n+2017\right)\) luôn chẵn
\(d,3^{200}=\left(3^2\right)^{100}=9^{100}>8^{100}=\left(2^3\right)^{100}=2^{300}\)

tại mình còn nhiều bài tập cần làm mai mình thi nên phải ôn nhiều bạn giúp mình nha ![]()
![]()

1.
$(a+b+c)-(a-b+c)=a+b+c-a+b-c=(a-a)+(b+b)+(c-c)=0+2b+0=2b$
2.
$(a-b+c)-(a-b+c)=0$
3.
$(a+b+c)-(b-a+c)=a+b+c-b+a-c=(a+a)+(b-b)+(c-c)=2a+0+0=2a$
4.
$(a-c)-(d+b+a+c)=a-c-d-b-a-c=(a-a)+(-c-c)-d-b=0-2c-d-b=-2c-d-b$
5.
$(a+d-c)-(a+b-c)=a+d-c-a-b+c=(a-a)+(-c+c)+d-b=0+0+d-b=d-b$
6.
$(a-b+c+d)+(a+c-d-b)=a-b+c+d+a+c-d-b$
$=(a+a)+(-b-b)+(c+c)+(d-d)=2a-2b+2c$
7.
$(a+d-c)+(a-b+c)=a+d-c+a-b+c=(a+a)+d+(-c+c)=2a+d$
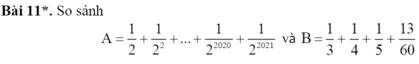

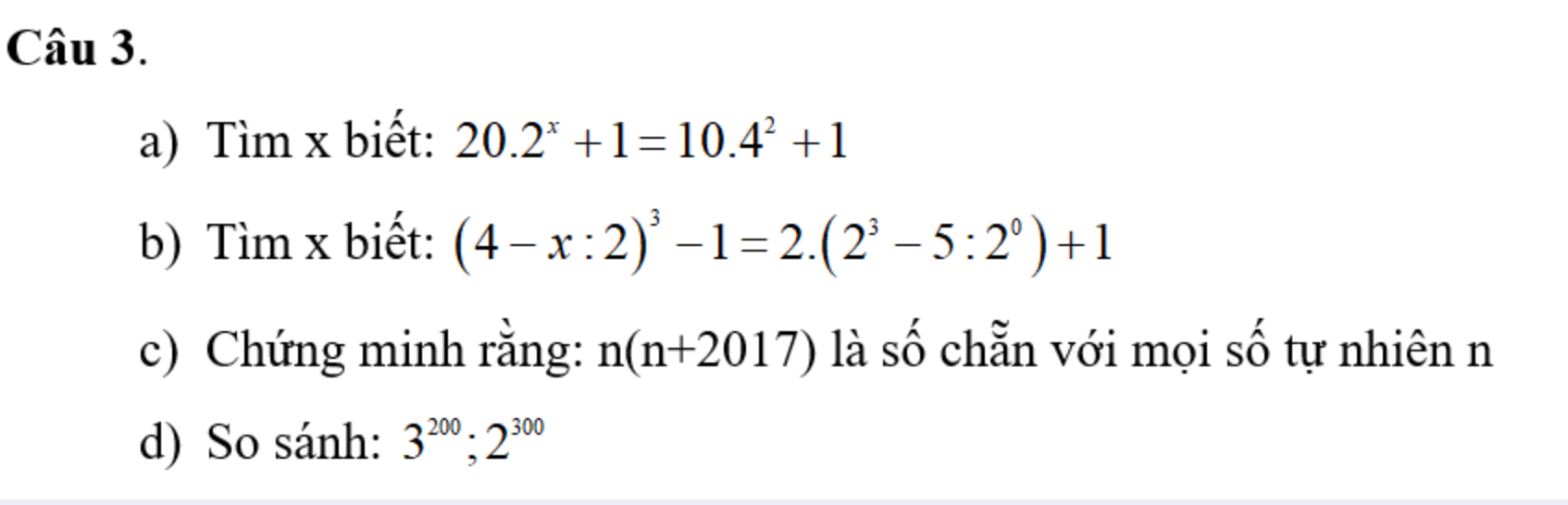 giúp mình với, mình cần gấp lắm, 5p phải nộp rồi
giúp mình với, mình cần gấp lắm, 5p phải nộp rồi
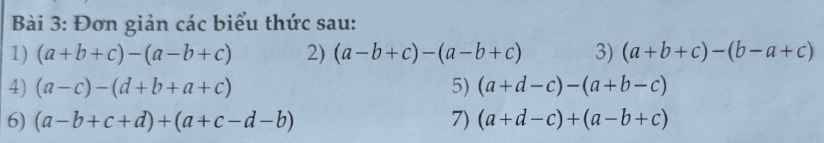
Giúp thế nào?
thiếu đề