Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,xét pt hoành độ gđ của (P)và (d) ta có
\(-4x^2\)=4mx+m2
<=>4x2+4m+m2=0(1)
ta có đen-ta phẩy=(2m)2-4m2=4m2-4m2=0
=>pt (1) có nghiệm kép
=>(P) luôn tiếp xúc vs (d) khi m thay đổi
b,xét pt hoành độ gđ của (P)và (d) ta có
x2=2(m-1)-2m+3
<=>x2-2(m-1)+2m-3=0(2)
ta có a+b+c=1-2m+2m-3=0
=> pt (2) luôn có 2 nghiệm x1=1;x2=2m-3
Vậy ..................
tớ làm hơi tắt mong cậu thông cảm ^-^

a, \(m=\dfrac{4}{3}\Leftrightarrow\left(d\right):y=-2:\dfrac{4}{3}\cdot x+2=-\dfrac{3}{2}+2\)
PT hoành độ giao điểm của (P) và (d) là
\(\dfrac{x^2}{2}=-\dfrac{3}{2}x+2\Leftrightarrow x^2=-3x+4\\ \Leftrightarrow x^2+3x-4=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=\dfrac{1}{2}\\y=8\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}A\left(1;\dfrac{1}{2}\right)\\B\left(-4;8\right)\end{matrix}\right.\)
Vậy \(A\left(1;\dfrac{1}{2}\right);B\left(-4;8\right)\) là tọa độ giao điểm của (P) và (d)
b, PT hoành độ giao điểm: \(\dfrac{x^2}{2}=-\dfrac{2}{m}x+2\Leftrightarrow x^2m=-4x+4m\)
\(\Leftrightarrow x^2m+4x-4m=0\left(1\right)\\ \Delta=16-4\left(-4m\right)m=16+8m^2>0,\forall m\)
Theo Vi-ét ta có \(x_1x_2=\dfrac{-4m}{m}=-4\) với \(x_1;x_2\) là nghiệm của (1)
Do đó \(x_1;x_2\) luôn trái dấu
Vậy PT(1) luôn có 2 nghiệm phân biệt trái dấu nên (P) luôn cắt (d) tại 2 điểm M,N nằm về 2 phía of trục tung
c, Gọi \(I\left(x_0;y_0\right)\) là điểm cố định mà (d) luôn đi qua
\(\Leftrightarrow y_0=-\dfrac{2}{m}\cdot x_0+2\Leftrightarrow my_0=-2x_0+2m\\ \Leftrightarrow m\left(y_0-2\right)+2x_0=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_0=0\\y_0=2\end{matrix}\right.\Leftrightarrow I\left(0;2\right)\)
Điểm C,D là ở đâu bạn nhỉ?

a) PT hoành dộ giao điểm d và (P):
x2-mx-m-1=0 (1). \(\Delta=\left(m+2\right)^2\)
d tiếp xúc với (P) <=> m=-2 tìm được x=-1
Tọa độ điểm A(-1;1)
b) Chỉ ra (1) luôn có nghiệm x=-1; x=m+1
Điều kiện để 2 giao điểm khác phía trục tung là:m >-1
Th1: với \(\hept{\begin{cases}x_1=-1\\x_2=m+1\end{cases}}\)tìm được m=\(\frac{-10}{3}\)(loại)
Th2: Với \(\hept{\begin{cases}x_1=m+1\\x_2=-1\end{cases}}\)tìm được m=0(tm)

a: 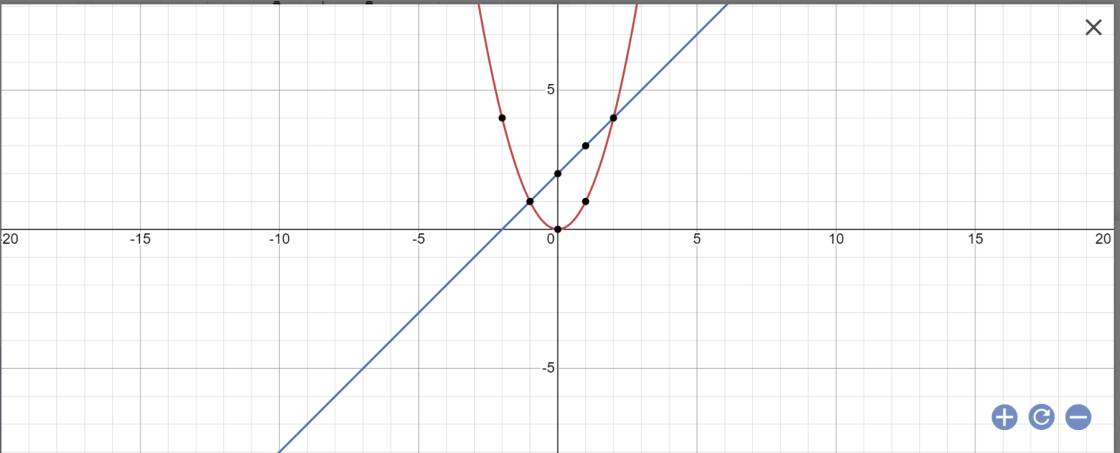
b: PTHĐGĐ là:
x^2-x-2=0
=>(x-2)(x+1)=0
=>x=2 hoặc x=-1
=>y=4 hoặc y=1
c: PTHĐGĐ là:
x^2-2x+m=0
Để (P) cắt (d1) tại hai điểm nằm về hai phía của trục tung thì m<0
Bài 2:
a: Phương trình hoành độ giao điểm là:
\(3x^2-5x+2=0\)
=>3x2-3x-2x+2=0
=>(x-1)(3x-2)=0
=>x=1 hoặc x=3/2
Do đó: (P) cắt (d) tại hai điểm nằm cùng phía với trục tung
b: Phương trình hoành độ giao điểm là:
\(-x^2-2x+2007=0\)(1)
a=-1; b=-2; c=2007
Vì ac<0 nên phương trình (1) có hai nghiệm trái dấu
Do đó: (P) cắt (d) tại hai điểm nằm về 2 phía đối với trục tung