
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\sqrt{3-x}\) - \(\sqrt{12-4x}\) + \(\sqrt{27-9x}\) = 20 đk \(3-x\) ≥ 0 ⇒ \(x\le3\)
\(\sqrt{3-x}\) - \(\sqrt{4.\left(3-x\right)}\) + \(\sqrt{9.\left(3-x\right)}\) = 20
\(\sqrt{3-x}\) - 2\(\sqrt{3-x}\) + 3\(\sqrt{3-x}\) = 20
\(\sqrt{3-x}\).( 1 - 2 + 3) = 20
2\(\sqrt{3-x}\) = 20
\(\sqrt{3-x}\) = 20: 2
\(\sqrt{3-x}\) = 10
3 - \(x\) = 100
\(x\) = 3 - 100
\(x\) = -97 (thỏa mãn)
Vậy \(x\) = -97

Gọi cường độ dòng điện qua bóng là I suy ra hiệu điện thế hai đầu bóng đèn là: \(U_đ=(\dfrac{I}{0,5})^2=4I^2\)
Hiệu điện thế giữa hai đầu điện trở là: \(U_R=I.R=240.I\)
Theo đề bài: \(U_đ+U_R=160\)
\(\Rightarrow 4I^2+240I=160\)
Giải pt trên ta tìm đc \(I=0,66A\)


a/ \(R_1=\frac{U_1}{I_1}=\frac{12}{2}=6\left(\Omega\right)\)
\(R_2=\frac{U_2}{I_2}=\frac{6}{1,5}=4\left(\Omega\right)\)
\(R_3=\frac{U_3}{R_3}=\frac{9}{1,5}=6\left(\Omega\right)\)
b/ \(R_{tđ}=R_1+\frac{R_2.R_3}{R_2+R_3}=6+\frac{4.6}{4+6}=8,4\left(\Omega\right)\)
\(I_1'=I_{23}'=\frac{U_{AB}}{R_{tđ}}=\frac{16,8}{8,4}=2\left(A\right)\)
\(\Rightarrow I_1'=I_1\Rightarrow\) đèn 1 sáng bình thường
\(U_{23}=U_2=U_3=U_{AB}-U_1=16,8-12=4,8\left(V\right)\)
\(\Rightarrow I_2'=\frac{U_2}{R_2}=\frac{4,8}{4}=1,2\left(A\right)< I_2\) \(\Rightarrow\) đèn 2 sáng yếu hơn bình thường
\(\Rightarrow I_3'=\frac{U_3}{R_3}=\frac{4,8}{6}=0,8\left(A\right)< I_3\Rightarrow\) đèn 3 sáng yếu hơn bình thường

điện trở tương đương của đoạn mạch là
Rtd=R1+R2+R3=10+10+15=35(\(\Omega\))
cường độ dòng điện của đoạn mạch là
I=\(\dfrac{U}{R}\)=\(\dfrac{24}{35}\)(\(\Omega\))
VÌ đây là mạch nối tiếp nên I=I1=I2=I3=\(\dfrac{24}{35}\)(\(\Omega\))
hiệu điện thế giưa hai đầu R1 là
U1=I1.R1=\(\dfrac{24}{35}.10=\dfrac{48}{7}\left(V\right)\)=R2
hiệu điện thế 2 đầu R3 là
U3=I3.R3=\(\dfrac{24}{35}.15=\dfrac{72}{7}\left(V\right)\)
mk nghĩ là vậy nếu đúng tick cho mình nha
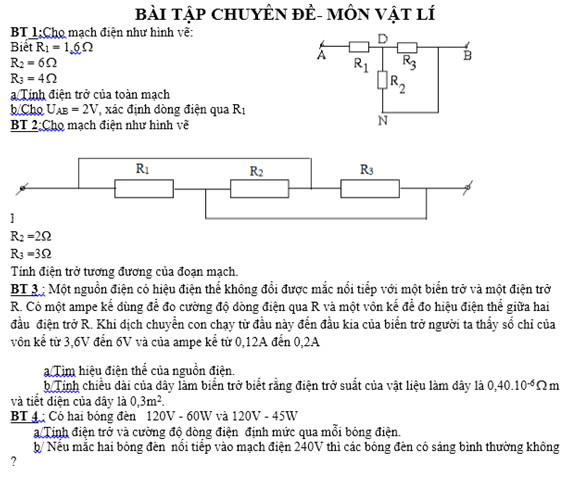 mng giúp mik bài 1 vs bài 3 vs, mik cần gấp lắm, cảm ơn mng.
mng giúp mik bài 1 vs bài 3 vs, mik cần gấp lắm, cảm ơn mng.
\(\sqrt{28-10\sqrt{3}}+\sqrt{28+10\sqrt{3}}\)
\(\sqrt{5^2-10\sqrt{3}+\sqrt{3}^2}+\sqrt{5^2+10\sqrt{3}+\sqrt{3}^2}\)
\(\sqrt{\left(5-\sqrt{3}\right)^2}+\sqrt{\left(5+\sqrt{3}\right)^2}\)
\(5-\sqrt{3}+5+\sqrt{3}=10\)
\(< =>ĐPCM\)