Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Tam giác ABC đều \(\Rightarrow OA=OB=OC\)
\(\Rightarrow\) Các tam giác OAB; OBC; OAC vuông cân tại O
\(\Rightarrow OA=OB=OC=\frac{AB}{\sqrt{2}}=a\)
\(V=\frac{1}{6}OA.OB.OC=\frac{a^3}{6}\)
Lời giải:
Đặt $AB=x$. Gọi $O$ là tâm đáy $ABCD$, $T$ là trung điểm $AB$
Ta có:
\(OT=\frac{BC}{2}=\frac{AB}{2}=\frac{x}{2}\) (tính chất đường trung bình)
$T$ là trung điểm $AB$, mà $SAB$ là tam giác đều nên $ST\perp AB$. Áp dụng đl Pitago:
\(ST^2=SB^2-BT^2=AB^2-(\frac{AB}{2})^2=x^2-(\frac{x}{2})^2=\frac{3}{4}x^2\)
Vì $S.ABCD$ là hình chóp đều nên $SO\perp (ABCD)\Rightarrow SO\perp OT$
Áp dụng đl Pitago: \(SO=\sqrt{ST^2-OT^2}=\sqrt{\frac{3}{4}x^2-(\frac{x}{2})^2}=\frac{x}{\sqrt{2}}\)
\(\Rightarrow S_{ABCD}=\frac{1}{3}.SO.S_{ABCD}=\frac{1}{3}.\frac{x}{\sqrt{2}}.x^2=\frac{a^3\sqrt{2}}{6}\)
\(\Rightarrow x=a\)
Vậy $AB=a$
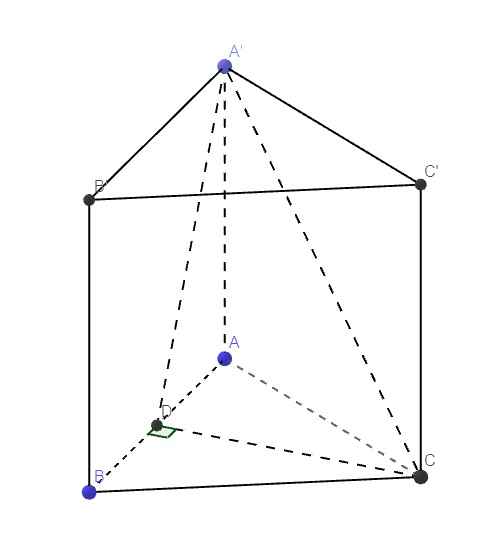
Gọi D là trung điểm AB \(\Rightarrow CD\perp AB\)
\(\Rightarrow CD\perp\left(AA'B'B\right)\)
\(\Rightarrow\widehat{CA'D}=30^0\)
\(CD=\dfrac{a\sqrt{3}}{2}\Rightarrow A'D=\dfrac{CD}{tan30^0}=\dfrac{3a}{2}\)
\(\Rightarrow A'A=\sqrt{CD^2-AD^2}=a\sqrt{2}\)
\(V=\dfrac{1}{3}A'A.S_{ABC}=\dfrac{1}{3}.a\sqrt{2}.\dfrac{a^2\sqrt{3}}{4}=\dfrac{a^3\sqrt{6}}{12}\)
Gọi E là trung điểm BC → AE vuông góc (vg) với BC
mà (ABC) vg (BB'C'C)
→ AE vg (BB'C'C)
\(V_{A.BB'C'C}=\frac{1}{3}\cdot AE\cdot S_{BB'C'C}=\frac{1}{3}\cdot\frac{a\sqrt{3}}{2}\cdot BB'\cdot BC=\frac{a^3\sqrt{3}}{3}\)
Vì SBB'C = 1/2 * SBB'C'C
nên VABB'C' = 1/2 * VA.BB'C'C = (a3căn3)/6
B A C H I S
Gọi H là trung điểm của BC, suy ra \(SH\perp BC\). Mà (SBC) vuông góc với (ABC) theo giao tuyến BC, nên \(SH\perp\left(ABC\right)\)
Ta có : \(BC=a\Rightarrow SH=\frac{a\sqrt{3}}{2}\); \(AC=BC\sin30^0=\frac{a}{2}\)
\(AB=BC.\cos30^0=\frac{a\sqrt{3}}{2}\)
Do đó \(V_{S.ABC}=\frac{1}{6}SH.AB.AC=\frac{a^3}{16}\)
Tam giác ABC vuông tại A và H là trung điểm của BC nên \(HA=HB\). Mà \(SH\perp\left(ABC\right)\), suy ra \(SA=SB=a\). Gọi I là trung điểm của AB, suy ra \(SI\perp AB\)
Do đó \(SI=\sqrt{SB^2-\frac{AB^2}{4}}=\frac{a\sqrt{13}}{4}\)
Suy ra \(d\left(C;\left(SAB\right)\right)=\frac{3V_{S.ABC}}{S_{SAB}}=\frac{6V_{S.ABC}}{SI.AB}=\frac{a\sqrt{39}}{13}\)
Chọn D
Từ giả thiết suy ra: ΔABC cân tại A có:
Gọi I là trung điểm của BC ⇒ A I ⊥ B C
Giả sử H là trực tâm của tam giác ABC.
Ta thấy O A ⊥ O B C
Vì O B ⊥ O A C ⇒ O B ⊥ A C và A C ⊥ B H nên A C ⊥ O B H ⇒ O H ⊥ A C ( 1 )
B C ⊥ O A I ⇒ O H ⊥ B C ( 2 )
Từ (1) và (2) suy ra O H ⊥ A B C
Có O I = 1 2 B C = a 2 2 = O A
=> ΔAOI vuông cân tại O => H là trung điểm AI và O H = 1 2 A I = a 2
Khi đó:
