Giúp Mình Với
Lester và Delbert làm việc tại một công ty điện tử. Họ hiện đang nghiên cứu một thành phần vi mạch dùng để kết nối hai phần độc lập của một siêu máy tính lớn. Thành phần này được xây dựng trên đầu của một breadboard - một cơ sở giống như lưới cho một vi mạch. Breadboard có n hàng và m cột, và mỗi giao điểm hàng-cột chứa một nút. Ngoài ra, ở mỗi bên của breadboard có các cổng có thể được gắn vào các nút liền kề. Bên trái và bên phải mỗi bên có n cổng, mỗi bên trên và dưới có m cổng. Mỗi cổng được kết nối ở bên ngoài với một trong các bộ phận được bắc cầu bởi bảng mạch, và có màu đỏ hoặc xanh lam tương ứng.
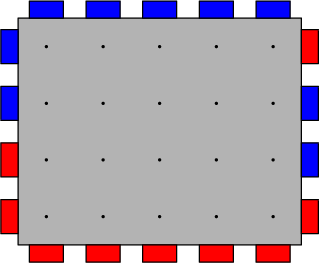
Các cổng có thể được kết nối bằng dây đi bên trong breadboard. Tuy nhiên, có một số quy tắc cần tuân theo: Mỗi dây phải kết nối một cổng màu đỏ với một cổng màu xanh lam và mỗi cổng phải được kết nối với nhiều nhất một dây. Mỗi phần của dây nên nằm ngang hoặc dọc và chỉ có thể quay ở một trong các nút. Để tránh nhiễu, dây không thể có các phần chung có độ dài khác 0 (nhưng có thể có các nút chung). Ngoài ra, một dây không thể bao phủ cùng một đoạn có chiều dài khác 0 hai lần. Dung lượng của breadboard là số lượng kết nối dây màu xanh lam đỏ lớn nhất có thể được thực hiện theo các quy tắc ở trên. Ví dụ: breadboard ở trên có dung lượng 7 và một cách để tạo bảy kết nối được minh họa bên dưới.
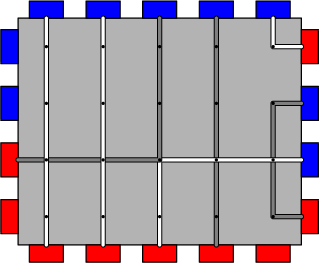
Cho đến thời điểm này các tuyên bố của cả hai phiên bản là giống hệt nhau. Sự khác biệt theo sau. Thông thường, các thông số kỹ thuật của dự án thay đổi rất nhiều trong quá trình phát triển, vì vậy màu sắc của các cổng vẫn chưa được cố định. Có q các sửa đổi để xử lý, mỗi trong số chúng có dạng "màu sắc của tất cả các cổng trong một phạm vi liền kề dọc theo một trong các bên được chuyển đổi (màu đỏ trở thành xanh lam và xanh lam trở thành đỏ)". Tất cả các sửa đổi đều tồn tại lâu dài, nghĩa là các sửa đổi trước đó không được hoàn tác trước khi sửa đổi tiếp theo được thực hiện. Để ước tính mức độ tồi tệ của những thay đổi, Lester và Delbert cần phải tìm dung lượng breadboard sau mỗi lần thay đổi. Giúp họ làm điều này một cách hiệu quả.
Đầu vào Dòng đầu tiên chứa ba số nguyên n, m, q (1≤n, m≤10 ^ 5, 0≤q≤10 ^ 5 ) - số hàng và cột của bảng mạch, và số lượng sửa đổi tương ứng. Bốn dòng tiếp theo mô tả màu ban đầu của các cổng. Mỗi ký tự trong các dòng này là R hoặc B, tùy thuộc vào màu của cổng tương ứng. Hai dòng đầu tiên chứa n mỗi ký tự và mô tả các cổng ở bên trái và bên phải tương ứng từ trên xuống dưới. Hai dòng cuối chứa m mỗi ký tự và mô tả các cổng ở phía trên và phía dưới tương ứng từ trái sang phải. Q tiếp theo dòng mô tả các sửa đổi. Mỗi dòng này chứa một ký tự s, theo sau là hai số nguyên l và r. Nếu s là L hoặc R, việc sửa đổi liên quan đến các cổng ở bên trái / bên phải tương ứng, l và r thỏa mãn 1≤l≤r≤n, và các cổng ở hàng giữa l và r (bao gồm) trên các màu chuyển đổi bên. Tương tự, nếu s là U hoặc D, thì 1≤l≤r≤m và các cổng trong cột giữa l và r (bao gồm) ở phía trên / dưới tương ứng chuyển đổi màu sắc.
Đầu ra In q + 1 số nguyên, một trên mỗi dòng - dung lượng bảng mạch sau khi sửa đổi 0,…, q đã được thực hiện đối với màu ban đầu.
INPUT
4 5 4
BBRR
RBBR
BBBBB
RRRRR
L 2 3
R 3 4
U 1 5
D 1 5
OUTPUT
7
7
9
4
9