Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

115.
+) 312312 là một hợp số
Ta thấy 312 là 1 số chẵn nên 312 ít nhất là chia hết cho số 2, tưc là 312 có ước là 2 khác với 1 và 312. Nên 312 là một hợp số.
+) 213213 là một hợp số.
giải thích: tổng các chữ số của 213213 là 2+1+3=62+1+3=6 chia hết cho 33 nên 213213 ⋮⋮ 33, nghĩa là 213213 có ước là 33, khác 11 và 213213 do đó nó là hợp số .
+) 435435 là một hợp số
giải thích: 435435 có chữ số tận cùng là 55 nên 435435 ⋮⋮ 55 nghĩa là 435435 có ước là 55 khác 11 và 435435 do đó nó là hợp số.
+) 417417 là một hợp số.
giải thích: 417417 có tổng các chữ số là 4+1+7=124+1+7=12 chia hết cho 33 nên 417417 ⋮⋮ 33, nghĩa là 417417 có ước là 33, khác 11 và 417417 do đó nó là hợp số.
+) 33113311 là một hợp số.
giải thích: 3311=11.3013311=11.301 nên 33113311 có ước là 1111 và 301301. Vậy 33113311 là một hợp số.
+) 6767 là một số nguyên tố vì nó chỉ có hai ước là 11 và 6767.
116.
83∈P83∈P, (vì 8383 chỉ có hai ước là 11 và chính nó)
9191 ∉∉ PP, (vì 9191 có các ước 1,7,13,911,7,13,91 do đó nó không phải số nguyên tố)
15∈N15∈N,
P⊂NP⊂N. (dựa vào định nghĩa số nguyên tố là số tự nhiên chỉ có hai ước là 11 và chính nó).
120.
5∗5∗¯
∗∈{0,1,2,3,4,5,6,7,8,9}∗∈{0,1,2,3,4,5,6,7,8,9}
Do đó ta xét ∗∗ với từng giá trị
+) Nếu ∗∈{0,2,4,6,8}∗∈{0,2,4,6,8} thì ¯¯¯¯¯¯5∗5∗¯ chia hết cho 22 do đó các trương hợp này không thỏa mãn.
+) Nếu ∗=5∗=5 thì 5555 chia hết cho 55 nên trường hợp này không thỏa mãn.
+) Nếu ∗=1∗=1 thì 5151 có tổng các chữ số là 5+1=65+1=6 chia hết cho 33 do đó 5151 chia hết cho 33, trường hợp này loại
+) Nếu ∗=3∗=3 thì 5353 là số nguyên tố
+) Nếu ∗=7∗=7 thì 5757 có tổng các chữ số là 5+7=125+7=12 chia hết cho 33 do đó 5757 chia hết cho 33, trường hợp này loại.
+) Nếu ∗=9∗=9 thì 5959 là số nguyên tố.
Vậy * = {3; 9}
¯¯¯¯¯¯9∗9∗¯
Tương tự ta xét như trên và tìm được số 9797 là số nguyên tố.
+) Nếu ∗∈{0,2,4,6,8}∗∈{0,2,4,6,8} thì ¯¯¯¯¯¯9∗9∗¯ chia hết cho 22 do đó các trương hợp này không thỏa mãn.
+) Nếu ∗=5∗=5 thì 9595 chia hết cho 55 nên trường hợp này không thỏa mãn.
+) Nếu ∗=1∗=1 thì 9191 chia hết cho 77 do đó trường hợp này loại.
+) Nếu ∗=3∗=3 thì 9393 có tổng các chữ số là 9+3=129+3=12 nên chia hết cho 3 do đó 9393 là hợp số, do đó trường hợp này loại.
+) Nếu ∗=7∗=7 thì 9797 là một số nguyên tố.
+) Nếu ∗=9∗=9 thì 9999 là một hợp số vì cỏ tổng các chữ số là: 9+9=189+9=18 chia hết cho 33 và 99. Do đó trường hợp này loại.
Vậy * = 7
122.
a) Đúng, vì có 22 và 33 là hai số tự nhiên liên tiếp đều là số nguyên tố;
b) Đúng, đó là 3,5,73,5,7;
c) Sai, vì 22 là số chẵn đồng thời cũng là số nguyên tố;
d) Sai vì 22 cũng là số nguyên tố.
Bài 115
312312 là một hợp số
Ta thấy 312 là 1 số chẵn nên 312 ít nhất là chia hết cho số 2, tưc là 312 có ước là 2 khác với 1 và 312. Nên 312 là một hợp số.
+) 213213 là một hợp số.
giải thích: tổng các chữ số của 213213 là 2+1+3=62+1+3=6 chia hết cho 33 nên 213213 ⋮⋮ 33, nghĩa là 213213 có ước là 33, khác 11 và 213213 do đó nó là hợp số .
+) 435435 là một hợp số
giải thích: 435435 có chữ số tận cùng là 55 nên 435435 ⋮⋮ 55 nghĩa là 435435 có ước là 55 khác 11 và 435435 do đó nó là hợp số.
+) 417417 là một hợp số.
giải thích: 417417 có tổng các chữ số là 4+1+7=124+1+7=12 chia hết cho 33 nên 417417 ⋮⋮ 33, nghĩa là 417417 có ước là 33, khác 11 và 417417 do đó nó là hợp số.
+) 33113311 là một hợp số.
giải thích: 3311=11.3013311=11.301 nên 33113311 có ước là 1111 và 301301. Vậy 33113311 là một hợp số.
+) 6767 là một số nguyên tố vì nó chỉ có hai ước là 11 và 6767.
Bài 116
83∈P83∈P, (vì 8383 chỉ có hai ước là 11 và chính nó)
9191 ∉∉ PP, (vì 9191 có các ước 1,7,13,911,7,13,91 do đó nó không phải số nguyên tố)
15∈N15∈N,
P⊂NP⊂N. (dựa vào định nghĩa số nguyên tố là số tự nhiên chỉ có hai ước là 11 và chính nó).
Bài 120
¯¯¯¯¯¯5∗5∗¯
∗∈{0,1,2,3,4,5,6,7,8,9}∗∈{0,1,2,3,4,5,6,7,8,9}
Do đó ta xét ∗∗ với từng giá trị
+) Nếu ∗∈{0,2,4,6,8}∗∈{0,2,4,6,8} thì ¯¯¯¯¯¯5∗5∗¯ chia hết cho 22 do đó các trương hợp này không thỏa mãn.
+) Nếu ∗=5∗=5 thì 5555 chia hết cho 55 nên trường hợp này không thỏa mãn.
+) Nếu ∗=1∗=1 thì 5151 có tổng các chữ số là 5+1=65+1=6 chia hết cho 33 do đó 5151 chia hết cho 33, trường hợp này loại
+) Nếu ∗=3∗=3 thì 5353 là số nguyên tố
+) Nếu ∗=7∗=7 thì 5757 có tổng các chữ số là 5+7=125+7=12 chia hết cho 33 do đó 5757 chia hết cho 33, trường hợp này loại.
+) Nếu ∗=9∗=9 thì 5959 là số nguyên tố.
Vậy * = {3; 9}
¯¯¯¯¯¯9∗9∗¯
Tương tự ta xét như trên và tìm được số 9797 là số nguyên tố.
+) Nếu ∗∈{0,2,4,6,8}∗∈{0,2,4,6,8} thì ¯¯¯¯¯¯9∗9∗¯ chia hết cho 22 do đó các trương hợp này không thỏa mãn.
+) Nếu ∗=5∗=5 thì 9595 chia hết cho 55 nên trường hợp này không thỏa mãn.
+) Nếu ∗=1∗=1 thì 9191 chia hết cho 77 do đó trường hợp này loại.
+) Nếu ∗=3∗=3 thì 9393 có tổng các chữ số là 9+3=129+3=12 nên chia hết cho 3 do đó 9393 là hợp số, do đó trường hợp này loại.
+) Nếu ∗=7∗=7 thì 9797 là một số nguyên tố.
+) Nếu ∗=9∗=9 thì 9999 là một hợp số vì cỏ tổng các chữ số là: 9+9=189+9=18 chia hết cho 33 và 99. Do đó trường hợp này loại.
Vậy * = 7
Bài 122
a) Đúng, vì có 22 và 33 là hai số tự nhiên liên tiếp đều là số nguyên tố;
b) Đúng, đó là 3,5,73,5,7;
c) Sai, vì 22 là số chẵn đồng thời cũng là số nguyên tố;
d) Sai vì 22 cũng là số nguyên tố.
k cho mk nha

125;
a;60 |2
30 |2
15 |3
5 |5
1
Do đó 60=2^2*3*5
b;84|2
42|2
21|3
7|7
1
Do đó 84=2^2*3*5
c; 285|3
95|5
19|19
1
Do đó 285=3*5*19
d; 1035|3
345|3
115|5
23|23
1
Do đó 1035=3^2*5*23
e; 400|2
200|2
100|2
50|2
25|5
5|5
1
Do đó 400=24*5^2
câu G bạn tự làm nha

Bài 125)
a)
![]()
Vậy: 60=22.3.560=22.3.5;
b)
![]()
Vậy: 84=22.3.784=22.3.7;
c)
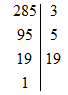
Vậy: 285=3.5.19285=3.5.19;
d)
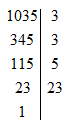
Vậy: 1035=32.5.231035=32.5.23;
e)
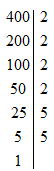
Vậy: 400=24.52400=24.52;
g) 1000000=26.561000000=26.56.
Vì 1000000=10.10.10.10.10.101000000=10.10.10.10.10.10
=2.5.2.5.2.5.2.5.2.5.2.5=2.5.2.5.2.5.2.5.2.5.2.5
Nên 1000000=2.5.2.5.2.5.2.5.2.5.2.5=26.561000000=2.5.2.5.2.5.2.5.2.5.2.5=26.56
Bài 127)
a)
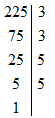
225=32.52225=32.52 chia hết cho 33 và 55;
b)

1800=23.32.521800=23.32.52 chia hết cho 2,3,52,3,5;
c)
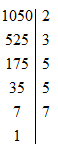
1050=2.3.52.71050=2.3.52.7 chia hết cho 2,3,5,72,3,5,7;
d)
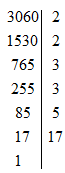
3060=22.32.5.173060=22.32.5.17 chia hết cho 2,3,5,172,3,5,17.
Bài 128)
44 là một ước của aa vì 44 là một ước của 2323;
8=238=23 là một ước của aa;
16=2416=24 không phải là ước của a;
1111 là một ước của aa;
2020 cũng là ước của aa vì 20=22.520=22.5 là ước của 23.5223.52.

cho tập hợp B={x,y,z}.Hỏi tập hợp B có bao nhiêu tập hợp con
bố mua cho em một quyển sổ tay dày 256 trang để tiện theo dõi em đánh số trang từ 1-256.Hỏi em phải viết bao nhiêu chữ số để đánh hết cuốn sổ tay
số nào là bội của 3 và là ước của 54
gọi A là tập hợp ước của 154.Hỏi A có số tập hợp con là

(149)@ ta có 60=2 mũ 2 nhân 3 nhân 5 280=2 mũ 3 nhân 5 nhân 7 BCNN (60,28 0)=2 mũ 3 nhân 3 nhân 5 nhân 7=840

ta có
12345678=1+2+3+4+5+6+7+8=36:hết cho 6(tổng 1 số chia hết 3 mà là số chẵn thì chia hết cho 6)
........
81234567: cho 6
=>biểu thức trên chia hết cho 6
Bạn j ơi, bạn hiểu sai ý mình rồi.
Ý mình là bạn phải tính biểu thức này cơ.
Chúc bạn may mắn lần sau.

Bài 139.
a) Ta có 56 = 23 . 7; 140 = 22 . 5 . 7. Do đó ƯCLN(56,140) = 22 . 7 = 28;
b) Ta có 24 = 23 . 3; 84 = 22 . 3 . 7; 180 = 22 . 32 . 5.
Vậy ƯCLN(24,84,180) = 22 . 3 = 12.
c) Vì 180⋮60 nên ƯCLN(60,180) = 60;
d) ƯCLN(15,19) = 1.
Bài 140.
a) Vì 80⋮16 và 176⋮16 nên ƯCLN(16, 80, 176) = 16;
b) Ta có 18 = 2 . 32 ; 30 = 2 . 3 . 5; 77 = 7 . 11.
Do đó 18 , 30, 77 không có ước chung nào khác 1.
Vậy ƯCLN(18,30,77) = 1.

0 = 2 - 2 + 2 - 2
1 = 2 : 2 + 2 - 2
2 = 2 : 2 + 2 : 2
3 = 2 + 2 - 2 : 2
4 = 2 + 2 + 2 - 2
k mình nha