K
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
14 tháng 8 2018
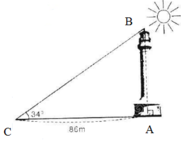
Gọi a là chiều cao của tháp, ta có:
\(\tan34\) = \(\dfrac{c.đối}{c.kề}\)= \(\dfrac{a}{86}\)
\(\Rightarrow a=\) \(\tan34.86\) \(\approx\) 58m
Vậy chiều cao của tháp là 58m
NL
1
CM
10 tháng 5 2018
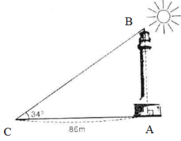
Kí hiệu đỉnh như hình vẽ. Theo hệ thức giữa các cạnh và góc của tam giác vuông, ta có:
A B = A C . t g 34 ° = 86 . t g 34 ° ≈ 58 ( m )
Vậy chiều cao tòa nhà là 58m.
CM
11 tháng 11 2019
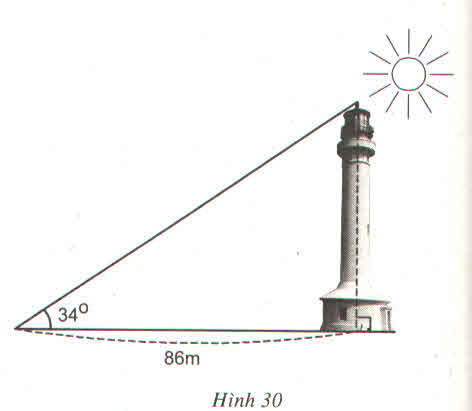
Kí hiệu đỉnh như hình vẽ. Theo hệ thức giữa các cạnh và góc của tam giác vuông, ta có:
AB = AC.tg34o = 86.tg34o ≈ 58 (m)
Vậy chiều cao tòa nhà là 58m.
6 tháng 6 2016
a) \(\sqrt[3]{27}-\sqrt[3]{-8}-\sqrt[3]{125}=\sqrt[3]{3^3}+\sqrt[3]{2^3}-\sqrt[3]{5^3}=3+2-5=0\)
b) \(\frac{\sqrt[3]{135}}{\sqrt[3]{5}}-\sqrt[3]{54}.\sqrt[3]{4}=\sqrt[3]{\frac{135}{5}}-\sqrt[3]{54.4}=\sqrt[3]{27}-\sqrt[3]{216}=3-6=-3\)
24 tháng 8 2019
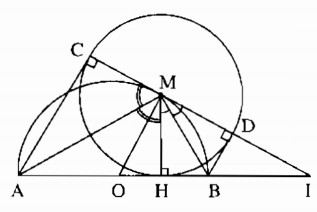
A B M H O C D I
a) Áp dụng tính chất hai tiếp tuyến giao nhau: ^HMC = 2.^AMH; ^HMD = 2.^BMH
Suy ra ^HMC + ^HMB = 2(^AMH + ^BMH) = 1800 => 3 điểm C,M,D thẳng hàng (đpcm).
Có C,M,D thẳng hàng, Do C,D thuộc (M;MH) nên CD là đường kính của (M;MH)
Khi đó MO là đường trung bình của hình thang vuông ACDB => MO // AC // BD
=> MO vuông góc CD => CD là tiếp tuyến của (O) (đpcm).
b) Dễ thấy AC + BD = AH + BH = 2R (R là bán kính của (O)) (không đổi).
c) Áp dụng hệ thức lượng trong tam giác vuông IMO có OH.OI = OM2 = R2 (không đổi).
6 tháng 6 2016
Giải:
a) \(\sqrt[3]{27}-\sqrt[3]{-8}-\sqrt[3]{125}=3-\left(-2\right)-5=3+2-5=0\)
b)\(\frac{\sqrt[3]{135}}{\sqrt[3]{5}}-\sqrt[3]{54}\cdot\sqrt[3]{4}=\frac{\sqrt[3]{27\cdot5}}{\sqrt[3]{5}}-\sqrt[3]{54\cdot4}=\frac{\sqrt[3]{27}\cdot\sqrt[3]{5}}{\sqrt[3]{5}}-\sqrt[3]{216}=3-6=-3\)
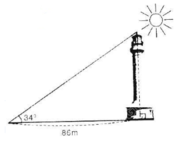
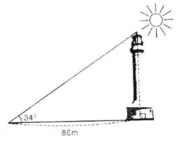
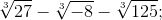
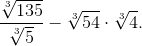
Gỉa sử chiều cao của tháp là BH , mặt đất là AH
Xét \(\Delta\)ABH , \(\widehat{H}\)= 90 \(^o\)
BH = AH tan 34\(^o\)
= 86 tan 34\(^o\)
\(\approx\) 58 m
Vậy chiều cao của tháp khoảng 58 m
ác tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng \(34^0\) và bóng của một tháp trên mặt đất dài 86m (h.30). Tính chiều cao của tháp (làm tròn đến mét)