Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

O x A B C
a) Chọn trục toạ độ như hình vẽ, gốc toạ độ trùng với vị trí A.
Chọn mốc thời gian lúc hai xe chuyển động.
+ Phương trình chuyển động của ô tô có dạng: \(x_1=x_0+v_0t+\dfrac{1}{2}at^2\)
\(x_0=0; v_0=10m/s; a=1m/s^2\)
Suy ra: \(x_1=10.t+0,5.t^2(m)\)
+ Phương trình chuyển động của xe máy có dạng: \(x_2=x_0+v.t\)
\(x_0=100m;v=15m/s\)
Suy ra: \(x_2=100+15.t(m)\)
b) Hai xe gặp nhau khi: \(x_1=x_2\)
\(\Rightarrow 10.t+0,5.t^2=100+15.t\)
\(\Rightarrow 0,5t^2-5t-100=0\)
\(\Rightarrow t = 20(s)\)
Thay t vào pt chuyển động ta có vị trí gặp nhau:
\(x=100+15.20=400(m)\)

giải:
a. Chọn chiều dương là chiều chuyển động của ô tô, gốc tọa độ tại vị trí xuất phát, gốc thời gian là lúc xe ô tô khởi hành.
Đối với xe ô tô:



Chọn chiều dương là chiều chuyển động của ô tô, gốc tọa độ tại vị trí xuất phát, gốc thời gian là lúc xe ô tô khởi hành.
Đối với xe ô tô:

Vậy hai xe gặp nhau sau 40s và cách gốc là 400m
Vận tốc ô tô:
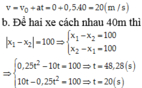

Chọn đáp án A
Lời giải:
+ Chọn chiều dương là chiều chuyển động của ô tô, gốc tọa độ tại vị trí xuất phát, gốc thời gian là lúc xe ô tô khởi hành.
+ Đối với xe ô tô:

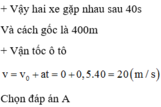

a) Chọn gốc tọa độ ở A. chiều dương hướng từ A->B.
Gốc thời gian là lúc hai xe bắt đầu xuất phát.
Phương trình chuyển động của hai xe lần lượt là
\(x_A=\:x_{0\:}+\:v_{0\:}t\)= 0+3t.
\(x_B=\: x_{0\: }+\: v_{0\: }t+\frac{1}{2}at^2=36+0.5.4t^2=36+2t^2.\)
b) Hai xa gặp nhau khi xA = xB
=> 3t = 36+2t^2
=> t = ...
Thay t vao x ta co vị trí gặp nhau.
*Chọn hệ quy chiếu
-Trục tọa độ trùng với đường thẳng AB
-Chiều dương (+) từ A đến B
-Gốc thời gian lúc hai xe xuất phát
-Gốc tọa độ tại điểm A
Giải
a) Phương trình chuyển động của hai xe
+ Xe ô tô chuyển động thẳng nhanh dần đều nên ta có phương trình
\(x_1=x_{o1}+v_{o1}.t+\dfrac{1}{2}.a.t^2\)
Với \(\left\{{}\begin{matrix}x_{o1}=0\\v_{o1}=10\\a=1\end{matrix}\right.\Rightarrow x_1=10t+0.5t^2\) (1)
+Xe máy chuyển động thẳng đều nên ta có phương trình
\(x_2=x_{o2}+v.\left(t-t_o\right)\)
Với \(\left\{{}\begin{matrix}x_{o2}=100\\v=5\\t_o=0\end{matrix}\right.\Rightarrow x_2=100+5t\) (2)
b) Vị trí và thời điểm hai xe gặp nhau là
\(x_1=x_2\)
hay: \(10t+0,5t^2=100+5t\)
\(\Rightarrow t=10\left(s\right)\)
Thay t=10(s) vào phương trình (1) và (2) ở trên ta được kết quả chung là 150m.
Vậy vị trí và thời điểm hai xe gặp nhau là 150m và 10s kể từ khi xuất phát.