Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B 1 2 3 4 1 2 3 4 a b c
a) Ta có các cặp góc đồng vị là: A1 và B1; A2 và B2 ; A3 và B3 ; A4 và B4
Giả sử đã cho : A1 = B1
ta có: A1 = A3 (đối đỉnh) ; B1 = B3 (đối đỉnh) => A3 =B3
Ta có: A1 + A2 = 180o (2 góc kề bù)
B1 + B2 = 180o (2 góc kề bù)
Mà A1 = B1 nên A2 = B2
Tương tự, A2 = A4 và B2 = B4 (đối đỉnh) nên A4 = B4
b) Các cặp góc so le trong là: A2 và B4 ; A3 và B1
Theo câu a) A2 = B2 mà B2 = B4 (do đối đỉnh) nên A2 = B4
Tương tư với A3 và B1
c) các cặp góc so le ngoài là: A1 và B3 ; A4 và B2
Ta có: A1 = B1 ( giả thiết) mà B1 = B3 (do đối đỉnh) => A1 = B3
A4 và B2 : tương tự
d) Các cặp góc trong cùng phía: A2 và B1 ; A3 và B4
Ta có: A1 + A2 = 180o (do kề bù)
Mà A1 = B1 nên B1 + A2 = 180o => A2 và B1 bù nhau
A3 và B4 : tương tự
e) các cặp góc ngoài cùng phía : A1 và B2 ; A4 và B3
Ta có: B1 + B2 = 180o ( do kề bù)
Mà A1 = B1 nên A1 + B2 = 180o => A1 và B2 bù nhau
A4 và B3 : tương tự

1.
a) bằng nhau
b) bằng nhau
c) bù nhau
2. bằng nhau; song song với nhau

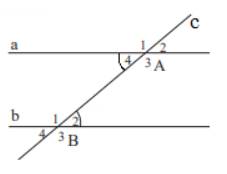
Vì đường thẳng c cắt hai đường thẳng a và b tạo thành một cặp góc so le trong ( góc A4 và B3) bằng nhau nên a // b ( Dấu hiệu nhận biết 2 đường thẳng song song)
Vì a // b nên theo tính chất của 2 đường thẳng song song:
a) Các so le trong bằng nhau
b) Các góc đồng vị bằng nhau
Mặt khác:
\(\left\{{}\begin{matrix}\widehat{A_1}+\widehat{A_2}=180^o\\\widehat{B_1}+\widehat{B_2}=180^o\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{A_1}=180^o-\widehat{A_2}\\\widehat{B_2}=180^o-\widehat{B_1}\end{matrix}\right.\) (hai cặp góc kề bù)
Mà \(\widehat{A_1}=\widehat{B_2}\) nên:
\(\widehat{A_2}=\widehat{B_1}\) Vậy nếu 1 đường thẳng cắt 2 đường thẳng mà trong các góc tạo thành có 1 cặp góc so le trong bằng nhau thì các cặp góc so le trong còn lại cũng bằng nhau.
Ta có: \(\widehat{A_1}=\widehat{B_2}\) (theo giả thiết)
Mặt khác:
\(\left\{{}\begin{matrix}\widehat{A_1}+\widehat{A_2}=180^o\\\widehat{B_1}+\widehat{B_2}=180^o\end{matrix}\right.\)(hai cặp góc kề bù)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{A_1}=180^o-\widehat{A_2}\\\widehat{B_2}=180^o-\widehat{B_1}\end{matrix}\right.\)
Mà \(\widehat{A_1}=\widehat{B_2}\) nên:
\(\widehat{A_2}=\widehat{B_1}\) hay cặp góc so le trong còn lại bằng nhau
Vậy nếu 1 đường thẳng cắt 2 đường thẳng mà trong các góc tạo thành có 1 cặp góc so le trong bằng nhau thì cặp góc so le trong còn lại cũng bằng nhau.