Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(2\sqrt{2}\left(\sqrt{3}-2\right)+\left(1+2\sqrt{2}\right)^2-2\sqrt{6}=9\)
Ta có : VT = \(2\sqrt{6}-4\sqrt{2}+1+4\sqrt{2}+8-2\sqrt{6}\)
\(\Leftrightarrow VT=9\) \(=VP\)
Vậy.........
b) \(\sqrt{2+\sqrt{3}}+\sqrt{2-\sqrt{3}}=\sqrt{6}\)
<=> \(\left(\sqrt{2+\sqrt{3}}+\sqrt{2-\sqrt{3}}\right)^2=6\)
Ta có : VT = \(2+\sqrt{3}+2-\sqrt{3}+2\sqrt{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}\)
= \(4+2\sqrt{4-3}=4+2=6\)
=> VT = VP
Vậy.....
c) \(\sqrt{\dfrac{4}{\left(2-\sqrt{5}\right)^2}}-\sqrt{\dfrac{4}{\left(2+\sqrt{5}\right)^2}}=8\)
Ta có : VT = \(\dfrac{\sqrt{4}}{\sqrt{\left(2-\sqrt{5}\right)^2}}-\dfrac{\sqrt{4}}{\sqrt{\left(2+\sqrt{5}\right)^2}}\)
= \(\dfrac{2}{\sqrt{5}-2}-\dfrac{2}{2+\sqrt{5}}=\dfrac{4+2\sqrt{5}-2\sqrt{5}+4}{\left(\sqrt{5}-2\right)\left(\sqrt{5}+2\right)}\)
= \(\dfrac{8}{5-4}=8\)
=> VT = VP
Vậy....
a) Biến đổi vế trái ta có:
VT= \(2\sqrt{2}\left(\sqrt{3}-2\right)+\left(1+2\sqrt{2}\right)^2-2\sqrt{6}\)
= \(2\sqrt{6}-4\sqrt{2}+1+4\sqrt{2}+8-2\sqrt{6}\)
= 9 = VP
Vậy đẳng thức đc chứng minh
b) Đặt vế trái = A = \(\sqrt{2+\sqrt{3}}+\sqrt{2-\sqrt{3}}\)
\(A^2=\left(\sqrt{2+\sqrt{3}}+\sqrt{2-\sqrt{3}}\right)^2\)
\(A^2=2+\sqrt{3}+2-\sqrt{3}+2.\sqrt{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}\)
\(A^2=4+2.\sqrt{4-3}=4+2.1=6\)
\(\Rightarrow A=\sqrt{6}=VP\)
Vậy đẳng thức đc chứng minh

a)\(\sqrt{\sqrt{5}-\sqrt{3-\sqrt{29-12\sqrt{5}}}}=1\)\(\Leftrightarrow\sqrt{\sqrt{5}-\sqrt{3-\sqrt{\left(2\sqrt{5}-3\right)^2}}}=1\)
\(\Leftrightarrow\sqrt{\sqrt{5}-\sqrt{3-2\sqrt{5}+3}}=1\)
\(\Leftrightarrow\sqrt{\sqrt{5}-\sqrt{6-2\sqrt{5}}}=1\)
\(\Leftrightarrow\sqrt{\sqrt{5}-\sqrt{\left(\sqrt{5}-1\right)^2}}=1\)
\(\Leftrightarrow\sqrt{\sqrt{5}-\sqrt{5}+1}=1\)
\(\Leftrightarrow\sqrt{1}=1\) (đpcm)

a: \(=\sqrt{5}+2+\sqrt{3}+1-\sqrt{5}-\sqrt{3}=3\)
b: \(=\left(-\sqrt{5}-2+\sqrt{5}-\sqrt{3}\right)\cdot\left(2\sqrt{3}+3\right)\)
\(=-\sqrt{3}\left(2+\sqrt{3}\right)\cdot\left(2+\sqrt{3}\right)\)
\(=-\sqrt{3}\left(7+4\sqrt{3}\right)=-7\sqrt{3}-12\)
c: \(=\dfrac{\sqrt{2}+\sqrt{3}+2}{\left(\sqrt{2}+\sqrt{3}+2\right)+\sqrt{2}\left(\sqrt{2}+\sqrt{3}+2\right)}=\dfrac{1}{1+\sqrt{2}}=\sqrt{2}-1\)

1/
\(\dfrac{3+2\sqrt{3}}{\sqrt{3}}+\dfrac{2+\sqrt{2}}{1+\sqrt{2}}-\dfrac{1}{2-\sqrt{3}}\)
\(=\dfrac{\sqrt{3}\left(\sqrt{3}+2\right)}{\sqrt{3}}+\dfrac{\sqrt{2}\left(\sqrt{2}+1\right)}{1+\sqrt{2}}-\dfrac{4-3}{2-\sqrt{3}}\)
\(=\sqrt{3}+2+\sqrt{2}-\dfrac{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}{2-\sqrt{3}}\)
\(=\sqrt{3}+2+\sqrt{2}-2-\sqrt{3}\)
\(=\sqrt{2}\)
2/
\(\left(\dfrac{\sqrt{6}-\sqrt{2}}{1-\sqrt{3}}-\dfrac{5}{\sqrt{5}}\right).\left(\sqrt{5}-\sqrt{2}\right)\)
\(=\left(\dfrac{\sqrt{2}\left(\sqrt{3}-1\right)}{1-\sqrt{3}}-\dfrac{\left(\sqrt{5}\right)^2}{\sqrt{5}}\right).\left(\sqrt{5}-\sqrt{2}\right)\)
\(=-\left(\dfrac{\left(\sqrt{5}\right)^2}{\sqrt{5}}-\dfrac{\sqrt{2}\left(\sqrt{3}-1\right)}{1-\sqrt{3}}\right).\left(\sqrt{5}-\sqrt{2}\right)\)
\(=-\left(\sqrt{5}+\sqrt{2}\right).\left(\sqrt{5}-\sqrt{2}\right)\)
\(=-\left(5-2\right)=-3\)
#F.C

2]\(\sqrt{3}\)+1+\(\sqrt{4-4\sqrt{3}+3}\)=\(\sqrt{3}+1+\sqrt{\left(2-\sqrt{3}\right)^2}=\sqrt{3}+1+2-\sqrt{3}=3\)
4\(\left(\dfrac{\sqrt{3}.\left(2+\sqrt{3}\right)+2.\left(2-\sqrt{3}\right)}{\left(2-\sqrt{3}\right).\left(2+\sqrt{3}\right)}\right)=\dfrac{\sqrt{3}.\left(2+\sqrt{3}\right)+2.\left(2-\sqrt{3}\right)}{1}\)
1: \(=2\sqrt{7}-12\sqrt{7}+15\sqrt{7}+27\sqrt{7}=32\sqrt{7}\)
3: \(=\sqrt{5}-2-\sqrt{14+6\sqrt{5}}\)
\(=\sqrt{5}-2-3-\sqrt{5}=-5\)
4: \(=2\sqrt{3}+3+4-2\sqrt{3}=7\)
5: \(=3-\sqrt{2}+3+\sqrt{2}+4-3=7\)
6: \(=\sqrt{\dfrac{6+2\sqrt{5}}{4}}+\sqrt{\dfrac{14-6\sqrt{5}}{4}}\)
\(=\dfrac{\sqrt{5}+1+3-\sqrt{5}}{2}=\dfrac{4}{2}=2\)
8: \(=\sqrt{5}-1+\sqrt{\dfrac{\left(3-\sqrt{5}\right)^2}{4}}-\sqrt{\dfrac{\left(3+\sqrt{5}\right)^2}{4}}\)
\(=\sqrt{5}-1+\dfrac{3-\sqrt{5}}{2}-\dfrac{3+\sqrt{5}}{2}\)
\(=\dfrac{2\sqrt{5}-2+3-\sqrt{5}-3-\sqrt{5}}{2}=\dfrac{-2}{2}=-1\)

Bài 2:
\(P=\left(\dfrac{\sqrt{a}}{2}-\dfrac{1}{2\sqrt{a}}\right)^2.\left(\dfrac{\sqrt{a}-1}{\sqrt{a}+1}-\dfrac{\sqrt{a}+1}{\sqrt{a}-1}\right)\)
\(P=\left(\dfrac{a-1}{2\sqrt{a}}\right)^2.\left(\dfrac{\left(\sqrt{a}-1\right)^2-\left(\sqrt{a}+1\right)^2}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\right)\)
\(P=\left[\dfrac{\left(a-1\right)^2}{4a}\right].\left(\dfrac{\left(\sqrt{a}-1+\sqrt{a}+1\right)\left(\sqrt{a}-1\right)-\sqrt{a}-1}{a-1}\right)\)
\(P=\dfrac{\left(a-1\right)^2}{4a}.\dfrac{2\sqrt{a}.\left(-2\right)}{a-1}\)
\(P=\dfrac{\left(a-1\right)^2\left(-4\sqrt{a}\right)}{4a.\left(a-1\right)}\)
\(P=\dfrac{\left(a-1\right).\left(-\sqrt{a}\right)}{a}=\dfrac{-a\sqrt{a}+\sqrt{a}}{a}\)
Bài 1:
\(A=\dfrac{2}{\sqrt{2}}-\dfrac{1}{\sqrt{3}-\sqrt{2}}+\dfrac{2}{\sqrt{3}-1}\)\(A=\dfrac{2\sqrt{2}}{2}-\dfrac{1\left(\sqrt{3}+\sqrt{2}\right)}{3-2}+\dfrac{2\left(\sqrt{3}+1\right)}{\left(\sqrt{3}\right)^2-1}\)
\(A=\sqrt{2}-\dfrac{\sqrt{3}+\sqrt{2}}{1}+\dfrac{2\left(\sqrt{3}+1\right)}{3-1}\)
\(A=\sqrt{2}-\sqrt{3}-\sqrt{2}+\sqrt{3}+1\)
\(A=1\)

♡
\(\dfrac{2}{1-\sqrt{2}}-\dfrac{2}{1+\sqrt{2}}\)
\(=\dfrac{2\left(1+\sqrt{2}\right)-2\left(1-\sqrt{2}\right)}{\left(1-\sqrt{2}\right)\left(1+\sqrt{2}\right)}\)
\(=\dfrac{2+2\sqrt{2}-2+2\sqrt{2}}{1-2}=-4\sqrt{2}\)
♡
\(\left(\dfrac{\sqrt{6}-\sqrt{2}}{1-\sqrt{3}}-\dfrac{5}{\sqrt{5}}\right)\left(\sqrt{5}-\sqrt{2}\right)\)
\(=\left[-\dfrac{\sqrt{2}\left(1-\sqrt{3}\right)}{1-\sqrt{3}}-\sqrt{5}\right]\left(\sqrt{5}-\sqrt{2}\right)\)
\(=-\left(\sqrt{5}+\sqrt{2}\right)\left(\sqrt{5}-\sqrt{2}\right)\)
\(=-3\)
♡
\(\dfrac{2}{7+4\sqrt{3}}+\dfrac{2}{7-4\sqrt{3}}\)
\(=\dfrac{2\left(7-4\sqrt{3}\right)+2\left(7+4\sqrt{3}\right)}{\left(7+4\sqrt{3}\right)\left(7-4\sqrt{3}\right)}\)
\(=\dfrac{14-8\sqrt{3}+14+8\sqrt{3}}{49-48}\)
= 28
♡
\(\dfrac{2}{\sqrt{5}+1}-\sqrt{\dfrac{2}{3-\sqrt{5}}}\)
\(=\dfrac{2}{\sqrt{5}+1}-\sqrt{\dfrac{4}{6-2\sqrt{5}}}\)
\(=\dfrac{2}{\sqrt{5}+1}-\dfrac{2}{\sqrt{\left(\sqrt{5}-1\right)^2}}\)
\(=\dfrac{2\left(\sqrt{5}-1\right)-2\left(\sqrt{5}+1\right)}{\left(\sqrt{5}+1\right)\left(\sqrt{5}-1\right)}\)
\(=\dfrac{2\sqrt{5}-2-2\sqrt{5}-2}{5-1}\)
= - 1
♡
\(\dfrac{4}{1-\sqrt{3}}-\dfrac{\sqrt{15}+\sqrt{3}}{1+\sqrt{5}}\)
\(=\dfrac{4\left(1+\sqrt{3}\right)}{1-3}-\dfrac{\sqrt{3}\left(\sqrt{5}+1\right)}{\left(\sqrt{5}+1\right)}\)
\(=-2-2\sqrt{3}-\sqrt{3}=-2-3\sqrt{3}\)
♡
\(\dfrac{\sqrt{2}}{2\sqrt{2}+\sqrt{3+\sqrt{5}}}\)
\(=\dfrac{2}{4+\sqrt{6+2\sqrt{5}}}\) (nhân [căn 2] vào cả tử và mẫu)
\(=\dfrac{2}{4+\sqrt{\left(\sqrt{5}+1\right)^2}}\)
\(=\dfrac{2}{5+\sqrt{5}}=\dfrac{2\left(5-\sqrt{5}\right)}{25-5}=\dfrac{5-\sqrt{5}}{10}\)



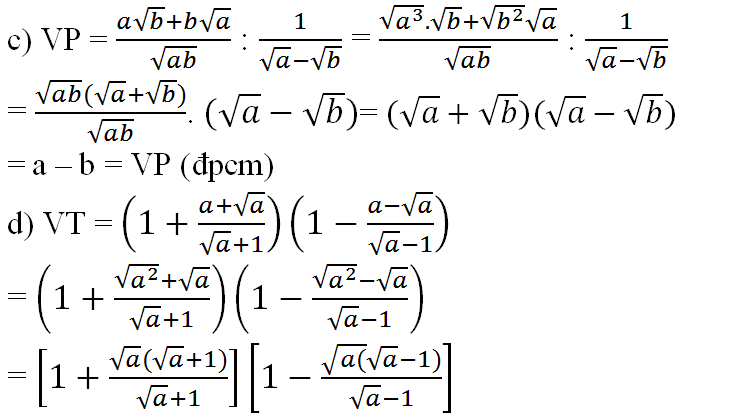
\(\left(\dfrac{\sqrt{6}-\sqrt{2}}{1-\sqrt{3}}-\dfrac{5}{\sqrt{5}}\right):\dfrac{1}{\sqrt{5}-\sqrt{2}}\)
\(=\left(\dfrac{-\sqrt{2}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}-\sqrt{5}\right)\cdot\left(\sqrt{5}-\sqrt{2}\right)\)
\(=\left(-\sqrt{2}-\sqrt{5}\right)\left(\sqrt{5}-\sqrt{2}\right)\)
\(=-\left(\sqrt{5}+\sqrt{2}\right)\left(\sqrt{5}-\sqrt{2}\right)=-\left(5-2\right)=-3\)