Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có cách tính diện tích ΔAOB với đường cao OM và cạnh đáy AB:
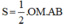
Ta lại có cách tính diện tích ΔAOB vuông với hai cạnh góc vuông OA, OB là:
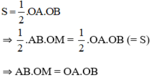

Dựng AH là đường cao của ΔABC, khi đó ΔABM,ΔAMC chung chiều cao AH. Ta có:
SAMB=12BM.AH
SAMC=12CM.AH
mà BM=CMBM=CM (vì AM là đường trung tuyến)
Vậy SAMB=SAMC.
S là diện -.-
Câu hỏi của Bảo bảo bối - Toán lớp 8 - Học toán với OnlineMath

a. xét tam giác ABC và tam giác HAC có
góc ACB= góc HCA ( góc chung)
góc BAC = góc AHC (=90độ)
do đó tam giác ABC đồng dạng với tam giác HAC(g.g)
b. theo bài ra ta có góc BAC=90 độ
suy ra tam giác ABC vuôg tại A
ta lại có AB=6cm, AC=8cm
suy ra AB ^2+ AC^2= BC^2
thay vào ta có 6^2+ 8^2= BC^2
suy ra BC^2= 10^2
suy ra BC = 10 (cm)

A A B B C C M M D D E E F F N N F' F'
a) Em tham khảo tại đây.
b) Trên tia đối tia FD, lấy điểm F' sao cho FF' = DE
Theo câu a ta có DF' = 2AM (1)
Lại có tứ giác ANDM có AN // DM, AM // DN nên ANDM là hình bình hành.
Vậy nên AM = ND (2)
Từ (1) và (2) suy ra NF' = ND
Lại có F'F = DE nên FN = EN hay N là trung điểm EF.
c) Ta có \(S^2_{FDC}\ge16S_{AMC}.S_{FNA}\Leftrightarrow\frac{S_{AMC}}{S_{FDC}}.\frac{S_{FNA}}{S_{FDC}}\le\frac{1}{16}\)
Ta thấy \(\frac{S_{AMC}}{S_{FDC}}=\left(\frac{MC}{DC}\right)^2;\frac{S_{FNA}}{S_{FDC}}=\left(\frac{AF}{FC}\right)^2\)
nên ta cần chứng minh \(\frac{MC}{DC}.\frac{AF}{FC}\le\frac{1}{4}\Rightarrow\frac{MC}{DC}.\left(1-\frac{AC}{FC}\right)\le\frac{1}{4}\)
\(\Rightarrow\frac{MC}{DC}.\left(1-\frac{MC}{DC}\right)\le\frac{1}{4}\)
Đặt \(\frac{MC}{DC}=x\Rightarrow x\left(1-x\right)=-x^2+x=\frac{1}{4}-\left(x-\frac{1}{2}\right)^2\le\frac{1}{4}\)
Vậy ta đã chứng minh xong.
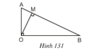
mỗi câu là một bài nha
câu 2
Dựng AH là đường cao của ΔABC, khi đó ΔABM,ΔAMC chung chiều cao AH. Ta có:
SAMB=12BM.AH
SAMC=12CM.AH
mà BM=CMBM=CM (vì AM là đường trung tuyến)
Vậy SAMB=SAMC.
S là diện -.-