
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Khoảng cách giữa 2 số lẻ liên tiếp là 2
Số lẻ đầu tiên là 1 thì số lẻ thứ n là:
\(1+\left(n-1\right).2=2n-1\)
Khi đó: tổng n STN lẻ liên tiếp kể từ 1 là:
\(1+3+5+...+\left(2n-1\right)\)
\(=\left(1+2n-1\right).n:2\)
\(=2n^2:2=n^2\)
Vậy tổng của n STN lẻ liên tiếp là số chính phương.
Chúc em học tốt.


2.
Gọi x;x+1;x+2;x+3 là 4 số tự nhiên liên tiếp ( x\(\in\) N)
Ta có : x (x+1) (x+2 ) (x+3 ) +1
=( x2 + 3x ) (x2 + 2x + x +2 ) +1
= ( x2 + 3x ) (x2 +3x + 2 ) +1 (*)
Đặt t = x2 + 3x thì (* ) = t ( t+2 ) + 1= t2 + 2t +1 = (t+1)2 = (x2 + 3x + 1 )2
=> x (x+1) (x+2 ) (x+3 ) +1 là số chính phương
hay tích 4 số tự nhiên liên tiếp cộng 1 là số chính phương
Gọi x;x+1;x+2;x+3 là 4 số tự nhiên liên tiếp ( x
∈
∈ N)
Ta có : x (x+1) (x+2 ) (x+3 ) +1
=( x2 + 3x ) (x2 + 2x + x +2 ) +1
= ( x2 + 3x ) (x2 +3x + 2 ) +1 (*)
Đặt t = x2 + 3x thì (* ) = t ( t+2 ) + 1= t2 + 2t +1 = (t+1)2 = (x2 + 3x + 1 )2
=> x (x+1) (x+2 ) (x+3 ) +1 là số chính phương
hay tích 4 số tự nhiên liên tiếp cộng 1 là số chính phương

Bài 1 :
Nếu n lẻ thì n + 1 chẵn do đó tổng n số tự nhiên liên tiếp là \(\frac{n.\left(n+1\right)}{2}\) là số chẵn nên không chia hết cho n vì n là số lẻ
Bài 2 :
Nếu n chẵn thì n + 1 lẻ do đó tổng n số tự nhiên liên tiếp là \(\frac{n.\left(n+1\right)}{2}\) là số chẵn nên chia hết cho n vì n là số chẵn

Giả sử 1^3+2^3+...+n^3=(1+2+...+n)^2(1)
Khi n=1 thì ta sẽ có 1^3=1^2(đúng)
Giả sử (1) đúng khi n=k
Khi n=2 thì ta sẽ có 1^3+2^3=9=(1+2)^2
Ta sẽ cần chứng minh (1) đúng khi n=k+1
1^3+2^3+...+n^3
=1^3+2^3+...+k^3+(k+1)^3
=(1+2+3+...+k)^2+(k+1)^3
Xét biểu thức (k+1)^2+2(k+1)(1+2+...+k)
=(k+1)^2+2*(k+1)*k*(k+1)/2
=(k+1)^2*(1+k)=(k+1)^3
=>1^3+2^3+...+(k+1)^3
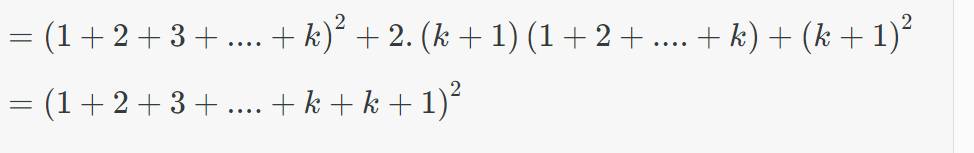
=>ĐPCM