K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LT
3
8 tháng 8 2017
\(S=5+5^2+5^3+.............+5^{2004}\)
\(\Leftrightarrow S=\left(5+5^4\right)+\left(5^2+5^5\right)+..........+\left(5^{2001}+5^{2004}\right)\) (\(1007\) nhóm)
\(\Leftrightarrow S=5\left(1+5^3\right)+5^2\left(1+5^3\right)+..........+5^{2001}\left(1+5^3\right)\)
\(\Leftrightarrow S=5.126+5^2.126+............+5^{2001}.126\)
\(\Leftrightarrow S=126\left(5+5^2+...........+5^{2001}\right)⋮126\)
\(\Leftrightarrow S⋮126\rightarrowđpcm\)
MV
8 tháng 8 2017
\(S=5+5^2+5^3+5^4+...+5^{2004}\\ =\left(5+5^3\right)+\left(5^2+5^4\right)+...+\left(5^{2001}+5^{2003}\right)+\left(5^{2002}+5^{2004}\right)\\ =5\cdot\left(1+5^2\right)+5^2\cdot\left(1+5^2\right)+...+5^{2001}\cdot\left(1+5^2\right)+5^{2002}\cdot\left(1+5^2\right)\\ =\left(1+5^2\right)\cdot\left(5+5^2+...+5^{2001}+5^{2002}\right)\\ =26\cdot\left(5+5^2+...+5^{2001}+5^{2002}\right)⋮26\)
Vậy \(S⋮26\)
DD
26 tháng 3 2016
a) Áp dụng bất đẳng thức Cauchy cho các số dương, ta có :
\(\log_23+\log_32>2\sqrt{\log_23.\log_32}=2\sqrt{1}=2\)
Không xảy ra dấu "=" vì \(\log_23\ne\log_32\)
Mặt khác, ta lại có :
\(\log_23+\log_32<\frac{5}{2}\Leftrightarrow\log_23+\frac{1}{\log_23}-\frac{5}{2}<0\)
\(\Leftrightarrow2\log^2_23-5\log_23+2<0\)
\(\Leftrightarrow\left(\log_23-1\right)\left(\log_23-2\right)<0\) (*)
Hơn nữa, \(2\log_23>2\log_22>1\) nên \(2\log_23-1>0\)
Mà \(\log_23<\log_24=2\Rightarrow\log_23-2<0\)
Từ đó suy ra (*) luôn đúng. Vậy \(2<\log_23+\log_32<\frac{5}{2}\)
b) Vì \(a,b\ge1\) nên \(\ln a,\ln b,\ln\frac{a+b}{2}\) không âm.
Áp dụng bất đẳng thức Cauchy ta có
\(\ln a+\ln b\ge2\sqrt{\ln a.\ln b}\)
Suy ra
\(2\left(\ln a+\ln b\right)\ge\ln a+\ln b+2\sqrt{\ln a\ln b}=\left(\sqrt{\ln a}+\sqrt{\ln b}\right)^2\)
Mặt khác :
\(\frac{a+b}{2}\ge\sqrt{ab}\Rightarrow\ln\frac{a+b}{2}\ge\frac{1}{2}\left(\ln a+\ln b\right)\)
Từ đó ta thu được :
\(\ln\frac{a+b}{2}\ge\frac{1}{4}\left(\sqrt{\ln a}+\sqrt{\ln b}\right)^2\)
hay \(\frac{\sqrt{\ln a}+\sqrt{\ln b}}{2}\le\sqrt{\ln\frac{a+b}{2}}\)
c) Ta chứng minh bài toán tổng quát :
\(\log_n\left(n+1\right)>\log_{n+1}\left(n+2\right)\) với mọi n >1
Thật vậy,
\(\left(n+1\right)^2=n\left(n+2\right)+1>n\left(n+2\right)>1\)
suy ra :
\(\log_{\left(n+1\right)^2}n\left(n+2\right)<1\Leftrightarrow\frac{1}{2}\log_{n+1}n\left(n+2\right)<1\)
\(\Leftrightarrow\log_{n+1}n+\log_{\left(n+1\right)}n\left(n+2\right)<2\)
Áp dụng bất đẳng thức Cauchy ta có :
\(2>\log_{\left(n+1\right)}n+\log_{\left(n+1\right)}n\left(n+2\right)>2\sqrt{\log_{\left(n+1\right)}n.\log_{\left(n+1\right)}n\left(n+2\right)}\)
Do đó ta có :
\(1>\log_{\left(n+1\right)}n.\log_{\left(n+1\right)}n\left(n+2\right)\) và \(\log_n\left(n+1>\right)\log_{\left(n+1\right)}\left(n+2\right)\) với mọi n>1
12 tháng 4 2020
Phương Linh Nguyễn Hoàng Bạn vt lại đề đc k ạ ? Sao mà AI vuông góc vs AB đc ạ ?
SG
1
20 tháng 5 2017
Gọi \(M_1\) là một mặt của hình đa diện (H). Gọi A, B, C là đỉnh liên tiếp của \(M_1\). Khi đó AB, BC là hai cạnh của (H). Gọi \(M_2\) làm mặt khác với \(M_1\) và có chung cạnh AB với \(M_1\). Khi đó \(M_2\) còn có ít nhất một đỉnh D khác với A và B. Nếu \(D\equiv C\) thì \(M_1\) và \(M_2\) có hai cạnh chung AB và BC, điều này vô lí.
Vậy D phải khác C. Do đó (H) có ít nhất bốn đỉnh A, B, C, D
HA
2
2 tháng 5 2016
Q(x)=x4+2015x2+2016
có: x4\(\ge\)0 với mọi x
2015x2 \(\ge\)0 với mọi x
2016>0
=> x4+2015x2+2016>0
Q(x) ko có nghiệm
LP
3
13 tháng 5 2020
bài làm
n*1=n
vì n/n=1 và n là số tự nhiên
C2:
xét 1*1=1
2*1=2
3*1=3
.
.
.
..
.
.
n*1=n
LT
0
22 tháng 3 2020
B A C D M
a, - Ta có : Tam giác ABC cân tại A .
=> AB = AC ( tính chất tam giác cân )
Mà AB = AD ( GT )
=> AB = AC = AD .
=> BD = BA + AD = 2AC .
=> AC = \(\frac{1}{2}BD\)
Vậy tam giác BCD vuông tại C ( tính chất đường trung tuyến trong tam giác vuông )
b, - Xét tam giác ADC có : AD = AC ( cmt )
=> Tam giác ADC cân tại A .
Mà AM là đườn phân giác .
=> AM là đường trung trực .
=> AM \(\perp\) DC .
Mà tam giác ADC vuông tại C .
=> BC \(\perp\) DC
=> AM // BC ( \(\perp\) DC )
15 tháng 5 2022
Tham khảo:
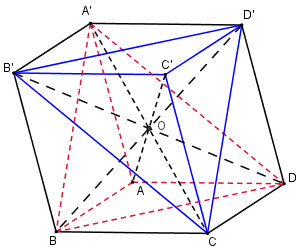
Xét 2 tứ diện A’ABD và CC’D’B’
Dùng phép đối xứng qua tâm O của hình hộp
Ta có:
A’ đối xứng C qua O
A đối xứng C’ qua O
B đối xứng D’ qua O
D đối xứng B’ qua O
Suy ra tứ diện A’ABD bằng tứ diện CC’D’B’.
26 tháng 3 2016
a) Ta có
\(a^2+4b^2=12ab\Leftrightarrow\left(a+2b\right)^2=16ab\)
Do a,b dương nên \(a+2b=4\sqrt{ab}\) khi đó lấy logarit cơ số 10 hai vế ta được :
\(lg\left(a+2b\right)=lg4+\frac{1}{2}lg\left(ab\right)\)
hay
\(lg\left(a+2b\right)-2lg2=\frac{1}{2}\left(lga+lgb\right)\)
b) Giả sử a,b,c đều dương khác 0. Để biểu diễn c theo a, ta rút lgb từ biểu thức \(a=10^{\frac{1}{1-lgb}}\) và thế vào biểu thức \(b=10^{\frac{1}{1-lgc}}\). Sau khi lấy logarit cơ số 10 2 vế, ta có :
\(a=10^{\frac{1}{1-lgb}}\Rightarrow lga=\frac{1}{1-lgb}\Rightarrow lgb=1-\frac{1}{lga}\)
Mặt khác , từ \(b=10^{\frac{1}{1-lgc}}\) suy ra \(lgb=\frac{1}{1-lgc}\) Do đó :
\(1-\frac{1}{lga}=\frac{1}{1-lgc}\)
\(\Rightarrow1-lgx=\frac{lga}{lga-1}=1+\frac{1}{lga-1}\)
\(\Rightarrow lgc=\frac{1}{1-lga}\)
Từ đó suy ra : \(c=10^{\frac{\frac{1}{1-lga}}{ }}\)
5.6 vẫn bằng 5.6 chứng minh đá rằng 26 không chia hết
de lam luon