
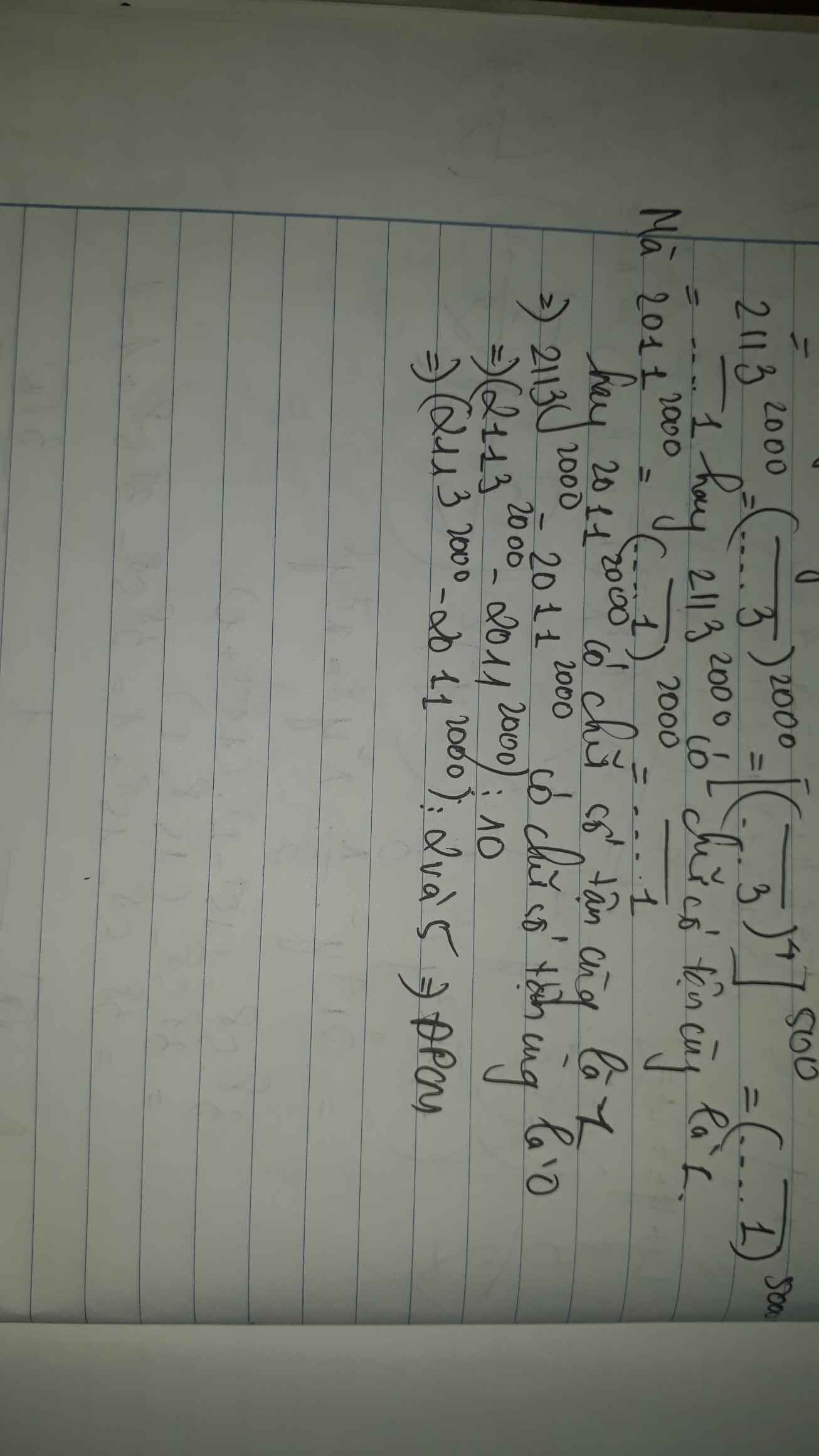
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

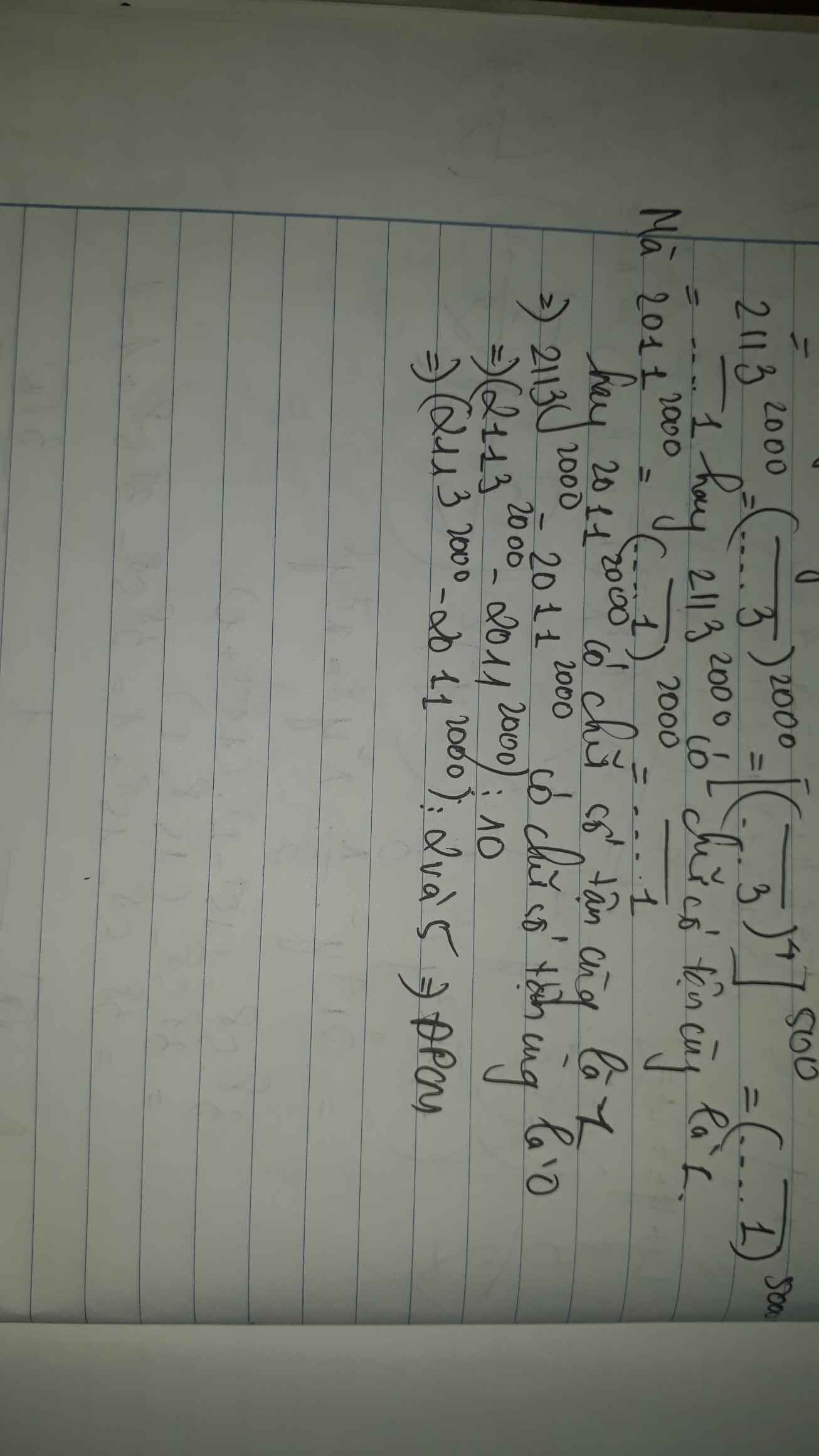

21132000 = 21134.500 nên 21132000 có chữ số tận cùng là 1
20392000 = 20392.1000 nên có chữ số tận cùng là 1
vì 1 - 1 = 0
nên 21132000 - 20392000 có chữ số tận cùng là 0
Vậy21132000 - 20392000 chia hết cho 2 và 5
9cm chuan 100000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000%

ab - ba = (10a + b) - (10b + a) = 10a + b - 10b - a = 9a - 9b = 9(a - b) chia hết cho 9
21132000 = (21134)500 = (...1)500 tận cùng là 1 ; 20112000 tận cùng là 1
=> 21132000 - 20112000 tận cùng là : 1 - 1 = 0 nên hiệu trên chia hết cho 2 và 5

\(2113^{2000}-2011^{2000}\)
\(=\left(2113^4\right)^{5000}-\left(2011^4\right)^{500}\)
\(=\left(....1\right)^{500}-\left(...1\right)^{500}\) vì \(3^4=81\)có tận cùng là 1; \(1^4=1\)(tương tự )
\(=\left(....0\right)\)chia hết cho 2 và 5\(\left(đpcm\right)\)

b;
bạn thử từng trường hợp đầu tiên là chia hết cho 2 thì n=2k và 2k+1.
.......................................................................3......n=3k và 3k + 1 và 3k+2
c;
bạn phân tích 2 số ra rồi trừ đi thì nó sẽ chia hết cho 9
d;tương tự b
e;g;tương tự a

Vì số chia hết cho cả 2 và 5 có tận cùng là 0.
Theo tính chất đã học ta có: \(2113^{2000}=2113^{4.500}=\left(...1\right)\) (1)
\(2031^{2000}=\left(...1\right)\) (2)
Từ (1) và (2) ta có: \(2113^{2000}-2031^{2000}=\left(...1\right)-\left(...1\right)=\left(...0\right)⋮2\) và \(5\Rightarrow\) đpcm

Cần chứng minh hiệu này chia hết cho 10
Ta có :
\(2999^{2013}-2011^{2000}=\left(...9\right)^{4.503}.\left(...9\right)-\left(...1\right)=\left(...1\right).\left(...9\right)-1=\left(....9\right)-1=\left(...8\right)\)không chia hết cho 10
Xem lại đề
29992013 = (...1)
20112000 = (...1)
=> 29992013 - 20112000 = (...0) chia hết cho 2 & 5 (đpcm)

20032000 có chữ số tận cùng là 1
20012000 có chữ số tận cùng là 1
1-1=0 nên 20032000 -20012000 chia hết cho 2 và 5
(20034)500-(20014)500=(....1)-(....1)=0=> 2003^2000-2001^2000 chia hết cho 2 và 5

2011^2002 = 2011^2000 . 2011^2 = (2011^5)^400 . 2011^2 = (.......5)^400 . ....1 = .....5 . ......1 = ........5 2009^2000 = (2009^5)^400 = tận cùng là 9 hoặc 1 vậy A ko chia hết cho 5 B = 2 + 2^2 + 2^3 + ..... + 2^100 2B = 2^2 + 2^3 +...................+ 2^101 B = 2^101 - 2 = 2^100 . 2 -2 = (2^4)^25 . 2 - 2 = 16^25 .2 - 2 = .....6 . 2 -2 = .......2 - 2 = .......0 vậy B chia hết cho 2

A=5+52+53+54+..........+52000
A=(5+52)+(53+54)+..............+(51999+52000)
A=5(1+5)+53(1+5)+................+51999(1+5)
A=(1+5).(5+53+.............+51999)
A=6.(5+53+...............+51999)⋮6
=> A⋮6