Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: ΔABC cân tại A(gt)
mà AF là đường trung tuyến ứng với cạnh đáy BC(do F là trung điểm của BC)
nên AF cũng là đường cao của ΔABC(định lí tam giác cân)
Xét tứ giác AFCO có
E là trung điểm của đường chéo AC(gt)
E là trung điểm của đường chéo OF(do O và F đối xứng nhau qua E)
Do đó: AFCO là hình bình hành(dấu hiệu nhận biết hình bình hành)
Xét hình bình hành AFCO có \(\widehat{AFC}=90\)độ(do AF⊥BC)
nên AFCO là hình chữ nhật(dấu hiệu nhận biết hình chữ nhật)
b)Xét ΔABC có
D là trung điểm của AB(gt)
E là trung điểm của AC(gt)
Do đó: DE là đường trung bình của ΔABC(định nghĩa đường trung bình của tam giác)
⇒\(DE\)//BC và \(DE=\frac{BC}{2}\)(định lí 2 về đường trung bình của tam giác)
Ta có: AF⊥BC(do AF là đường cao của ΔABC)
mà DE//BC(cmt)
nên DE⊥AF(định lí 2 về quan hệ giữa vuông góc và song song)
Ta có: AO=FC(do AO và FC là hai cạnh đối của hình chữ nhật AOCF)
mà FC=BF(do F là trung điểm của BC)
nên AO=BF(1)
Ta có: \(DE=\frac{BC}{2}\)(cmt)
mà \(FC=BF=\frac{BC}{2}\)(do F là trung điểm của BC)
nên DE=BF=FC(2)
Từ (1) và (2) suy ra AO=DE
Ta có: AB=AC(do ΔABC cân tại A)
mà AC=FO(do AC và FO là hai đường chéo của hình chữ nhật AOFC)
nên AB=FO
\(\Rightarrow\frac{AB}{2}=\frac{FO}{2}\)(3)
mà \(AD=\frac{AB}{2}\)(do D la trung điểm của AB) (4)
và \(OE=\frac{FO}{2}\)(do E là trung điểm của FO) (5)
nên từ (3),(4),(5)suy ra AD=OE
Xét tứ giác ADEO có AD=OE(cmt) và AO=DE(cmt)
nên ADEO là hình bình hành(dấu hiệu nhận biết hình bình hành)
\(\Rightarrow AE\) và DO cắt nhau tại trung điểm mỗi đường
mà \(AE\cap DE=\left\{P\right\}\)(gt)
nên P là trung điểm của AE
Ta có: DE//BC(cmt)
mà F∈BC(do F là trung điểm của BC)
nên DE//FC
Xét tứ giác DECF có
DE//FC(cmt) và DE=FC(cmt)
nên DECF là hình bình hành(dấu hiệu nhận biết hình bình hành)
⇒2 đường chéo DC và FE cắt nhau tại trung điểm của mỗi đường(định lí hình bình hành)
mà \(DC\cap FE=\left\{Q\right\}\)(gt)
nên Q là trung điểm của FE
Xét ΔEAF có
P là trung điểm của AE(cmt)
Q là trung điểm của FE(cmt)
Do đó: FQ là đường trung bình của ΔEAF(định nghĩa đường trung bình của tam giác)
⇒FQ//AF(định lí 2 về đường trung bình của tam giác)
Ta có: DE⊥AF(cmt)
FQ//AF(cmt)
Do đó: DE⊥FQ(định lí 2 về quan hệ giữa vuông góc và song song)(đpcm)
Wow, dài thế
Cảm ơn bạn nhiều vì đã bỏ công giúp mình nhé ![]()

Bạn có thể chụp hình mình xem với không??,
Chỗ mk PQ không vuông góc với AE
1: Xét tứ giác AFCO có
E là trung điểm chung của AC và FO
nên AFCO là hình bình hành
mà góc AFC=90 đô
nên AFCO là hình chữ nhật
2: Xét ΔABC có AD/AB=AE/AC
nên DE//BC và DE=1/2BC=FC=AO
=>DE//AO và DE=AO
=>AOED là hình bình hành
3: Sửa đề; Cm PQ vuông góc với DE
Xét tứ giác DECF có
DE//CF
DE=CF
Do đó: DECF là hình bình hành
=>Q là trung điểm của DC
Xét ΔDOC co DP/DO=DQ/DC
nên PQ//OC
=>PQ vuông góc với DE
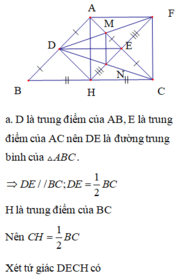


1) ΔABC cân tại A ; AF là trung tuyến ( F là trung điểm BC )
\(\Rightarrow\) AF đồng thời là đường cao \(\Rightarrow\) \(\widehat{AFC}\) = 90\(^O\)
Xét tứ giác AFCO có :
AE = EC ( E là trung điểm AC )
EF = OE ( O đối xứng với F qua E )
AC \(\cap\) OF = \(\left\{E\right\}\)
\(\Rightarrow\) AFCO là hình bình hành
mà \(\widehat{AFC}\) = 90O (cmt) \(\Rightarrow\) AFCO là hình chữ nhật
2) a) Xét ΔABC có :
BF = CF ( F là trung điểm BC )
AE = CE ( E là trung điểm AC )
\(\Rightarrow\) EF là đường trung bình ΔABC
\(\Rightarrow\) EF // AB ; EF = \(\dfrac{1}{2}\) AB ( Tính chất đường trung bình trong tam giác )
CMTT : DE là đường trung binh ΔABC
\(\Rightarrow\) DE // BC ( Tính chất đường trung bình tỏng tam giác )
EF = EO = \(\dfrac{1}{2}\) AB ( cmt ) ; AD = \(\dfrac{1}{2}\) AB ( D là trung điểm AB )
\(\Rightarrow\) EO = AD
Xét tứ giác ADEO có :
EO = AD ( cmt )
EO // AD ( EF // AD )
\(\Rightarrow\) ADEO là hình bình hành \(\Rightarrow\) AP = EP
CMTT : DECF là hình bình hành \(\Rightarrow\) EQ = FQ
b) DE // BC (cmt) ; AF\(\perp\)BC ( \(\widehat{AFC}\) = 90O )
\(\Rightarrow\) DE \(\perp\) AF
Xét ΔAEF có :
AP = EP (cmt)
EQ = FQ (cmt)
\(\Rightarrow\) PQ là đường trung bình ΔAEF
\(\Rightarrow\) PQ // AF (Tính chất đường trung bình trong tam giác)
mà DE \(\perp\) AF (cmt) \(\Rightarrow\) PQ \(\perp\) DE