
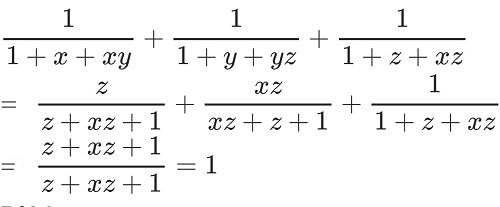
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

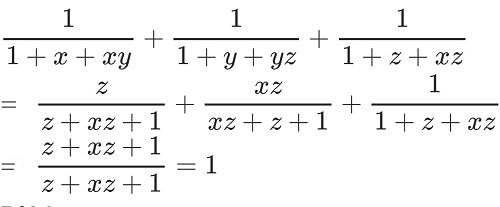

\(A=\dfrac{x}{xy+x+1}+\dfrac{y}{y+1+yz}+\dfrac{z}{1+z+xz}\)
\(=\dfrac{x}{xy+x+xyz}+\dfrac{y}{y+1+yz}+\dfrac{yz}{1+yz+z}\)
\(=\dfrac{x}{x\left(y+1+yz\right)}+\dfrac{y}{y+1+yz}+\dfrac{yz}{1+yz+y}\)
\(=\dfrac{1}{y+1+yz}+\dfrac{y}{y+1+yz}+\dfrac{yz}{1+yz+y}\)
\(=\dfrac{1+y+yz}{y+1+yz}=1.\)

Đặt biểu thức trên là A, thay xyz = 2018, ta dược :
\(A=\dfrac{x^2yz}{xy+xyz+x^2yz}+\dfrac{y}{yz+y+xyz}+\dfrac{z}{xz+x+1}\)
\(=\dfrac{xy\left(xz\right)}{xy\left(1+z+xz\right)}+\dfrac{y}{y\left(z+1+xz\right)}+\dfrac{z}{z+zx+1}\)
\(=\dfrac{xz}{1+z+xz}+\dfrac{1}{z+1+xz}+\dfrac{z}{z+zx+1}=\dfrac{xz+1+z}{1+z+xz}=1\)
⇒ĐPCM
Please help me!!!!!!!!!!!![]()
![]()
![]()
I feel this exercise is difficult!!!!!!![]()

\(P=\frac{1}{1+x+xy}+\frac{1}{1+y+yz}+\frac{1}{1+z+xz}.\)
\(P=\frac{1}{1+x+xy}+\frac{x}{x\left(1+y+yz\right)}+\frac{xy}{xy\left(1+z+xz\right)}\)
\(P=\frac{1}{1+x+xy}+\frac{x}{x+xy+xyz}+\frac{xy}{xy+xyz+x^2yz}\)
\(P=\frac{1}{1+x+xy}+\frac{x}{x+xy+xyz}+\frac{xy}{xy+xyz+xyz.x}\)
\(P=\frac{1}{1+x+xy}+\frac{x}{x+xy+1}+\frac{xy}{xy+1+x}\left(xyz=1\right)\)
\(P=\frac{1+x+xy}{1+x+xy}=1\)
Vậy P=1

\(A=\frac{x}{xy+x+1}+\frac{y}{y+1+yz}+\frac{z}{1+z+xz}\)
\(=\frac{x}{xy+x+1}+\frac{xy}{xy+x+xyz}+\frac{xyz}{xy+xyz+x^2yz}\)
\(=\frac{x}{xy+x+1}+\frac{xy}{xy+x+1}+\frac{1}{xy+1+x}\)
\(=\frac{xy+x+1}{xy+x+1}=1\)
\(\frac{x}{xy+x+1}+\frac{xy}{yx+x+xyz}+\frac{xyz}{xy+xyz+x^2yz}\)
\(\frac{x}{xy+x+1}+\frac{xy}{yx+x+1}+\frac{1}{xy+1+x}\)
\(\frac{x+xy+1}{xy+x+1}=1\)

\(\dfrac{1}{xy+x+1}+\dfrac{y}{yz+y+1}+\dfrac{1}{xyz+yz+y}\)
\(=\dfrac{xyz}{xy+x+xyz}+\dfrac{y}{yz+y+1}+\dfrac{1}{yz+y+1}\)
\(=\dfrac{xyz}{x\left(y+1+yz\right)}+\dfrac{y}{yz+y+1}+\dfrac{1}{yz+y+1}\)
\(=\dfrac{yz}{yz+y+1}+\dfrac{y}{yz+y+1}+\dfrac{1}{yz+y+1}\)
\(=\dfrac{yz+y+1}{yz+y+1}=1\left(đpcm\right)\)
Vậy...
êu , sao \(\dfrac{1}{xy+x+1}\)+... lại bằng \(\dfrac{xyz}{xy+z+zxy}\)+... vậy ?

TA CÓ \(\frac{x}{xy+x+1}\)+\(\frac{y}{yz+y+1}\)+\(\frac{z}{xz+z+1}\)
=\(\frac{x}{xy+x+1}\)+\(\frac{xy}{xyz+xy+x}\)+\(\frac{xyz}{x^2yz+xyz+xy}\)
=\(\frac{x}{xy+x+1}\)+\(\frac{xy}{xy+x+1}\)+\(\frac{1}{xy+x+1}\)(vì xyz=1)
=\(\frac{x+xy+1}{xy+x+1}\)
= 1