Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi M là trung điểm của AF . Ta có OM là đường trung bình của tam giác ACF
\(=>OM//CF,OM=\frac{1}{2}CF\)
ta lại có \(OM//CF,CF\perp CD\left(gt\right)\)
\(=>OM\perp CD.Mà\left(AB//CD\right)\)
\(=>OM//BE\)(1)
mặt khác OM , AM là 2 đường cao của tam giác ABO
=> M là trực tâm của tam giác ABO
=>\(BM\perp AC.Mà\left(EO\perp AC\right)=>BM//EO\left(2\right)\)
từ 1 zà 2 => tứ giác BMOE là hbh => OM=BE
ta có
\(OM=BE;OM=\frac{1}{2}CF=>BE=\frac{1}{2}CF\left(and\right)BE//OM//CF\)
\(\Delta KCF\)có \(CF//BE=>\frac{KE}{KF}=\frac{BE}{CF}=\frac{1}{2}\)

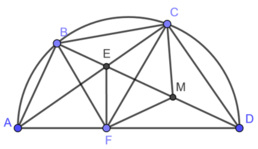
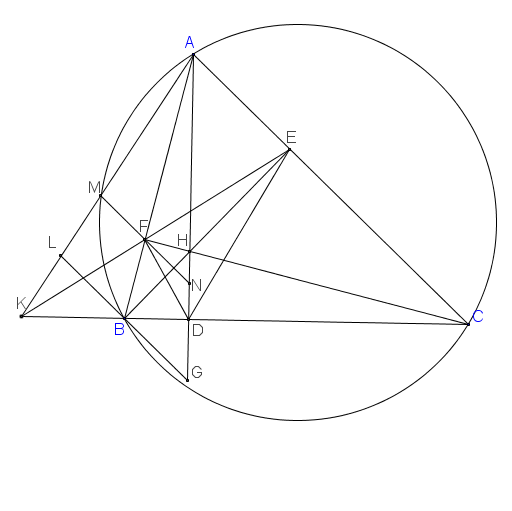
Xét $(O)$ có: $\widehat{ACD}=\widehat{ABD}=90^o$( góc nội tiếp chắn nửa đường tròn)
suy ra $\widehat{ECD}=90^o$
$\widehat{BAC}=\widehat{BDC}$ (các góc nội tiếp cùng chắn cung $BC$)
hay $\widehat{BAE}=\widehat{EDC}(1)$
Xét tứ giác $BEFA$ có: $\widehat{ABE}=\widehat{EFA}=90^o$ (do $EF AD$)
nên $\widehat{ABE}+\widehat{EFA}=180^o$
suy ra tứ giác $BEFA$ nội tiếp
suy ra $\widehat{EFB}=\widehat{BAE}(2)$ (các góc nội tiếp cùng nhắn $BE$)
Chứng minh tương tự ta có: tứ giác $ECDF$ nội tiếp nên $\widehat{EFC}=\widehat{EDC}(3)$ (các góc nội tiếp cùng chắn cung $EC$)
Từ $(1)(2)(3)$ suy ra $\widehat{EFB}+\widehat{EFC}=\widehat{BAE}+\widehat{EDC}=2.\widehat{EDC}$
hay $\widehat{BFC}=2.\widehat{EDC}$
Lại có: tam giác $ECD$ vuông tại $C$
$M$ là trung điểm $ED$
Nên $EM=MD=CM$
Suy ra tam giác $MCD$ cân tại $M$
nên $\widehat{MCD}=\widehat{MDC}$
Lại có: $\widehat{BMC}$ là góc ngoài tam giác $MCD$ nên
$\widehat{BMC}=\widehat{MCD}+\widehat{MDC}=2.\widehat{MDC}=2.\widehat{EDC}
Mà $\widehat{BFC}=2.\widehat{EDC}$
nên $\widehat{BMC}=\widehat{BFC}$
suy ra $F;M$ cùng nhìn đoạn $BC$ dưới 1 góc ko đổi
$F;M$ là 2 đỉnh liên tiếp tứ giác $BCMF$
suy ra tứ giác $BCMF$ nội tiếp (Bài toan quỹ tích cung chứa góc)

Xét tam giác vuông EFD có:
FM là đường trung tuyến ứng với cạnh huyền CD
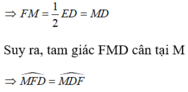
Ta có:
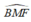 là góc ngoài tại đỉnh M của tam giác FMD nên:
là góc ngoài tại đỉnh M của tam giác FMD nên:

Xét tứ giác BCMF có:
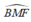 và
và  và cùng nhìn cạnh BF dưới một góc bằng nhau
và cùng nhìn cạnh BF dưới một góc bằng nhau
Suy ra, tứ giác BCMF nội tiếp được.

Gọi K là giao của MI và AD
góc CIM=góc IAM+góc IMA
ΔBIC vuông tạiI có IM là trung tuyến
nên góc CIM=góc ICM=góc ACB
=>góc KAM+góc AMK=góc DAC+góc IAM+góc IMA
=90 độ
=>MI vuông góc AD
EF ạ