Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Ta có A C → = 0 ; - 2 ; 4 ; A B → = 1 ; - 1 ; 2 ⇒ A C → ; A B → = 0 ; 4 ; 2 .
D nằm trên trục Oy nên D = 0 ; d ; 0 .
Cách 1:
Ta có A D → = - 2 ; d - 1 ; 1 ; A C → ; A B → A D → = 4 d - 1 + 2 = 4 d - 2 .
V A B C D = 1 6 A C → ; A B → A D → ⇒ 1 6 4 d - 2 = 5 ⇒ 4 d - 2 = 30 4 d - 2 = 30 ⇒ d = 8 d = - 7 .
Từ đó ta chọn A.
Cách 2:
S A B C = 1 2 A C → , A B → = 5 .
V = 5 = 1 3 . S A B C . d D ; A B C ⇒ d D ; A B C = 3 5 .
Mặt phẳng A B C : đi qua A 2 ; 1 ; - 1 và có vtpt n → = 0 ; 4 ; 2 .
⇒ A B C : 4 y - 1 + z + 1 = 0 ⇔ 2 y - 2 + z + 1 = 0 ⇔ 2 y + z - 1 = 0
d D ; A B C = 2 . d - 1 5 = 3 5 ⇔ d = 8 d = - 7 . Vậy ta chọn A.

Đáp án D.
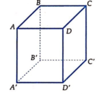
Cách 1: Do A B C D . A ' B ' C ' D ' là hình hộp nên ta có
B C → = A D → = 0 ; − 1 ; 0 ⇒ x C = 0 + 2 = 2 y C = − 1 + 1 = 0 z C = 0 + 2 = 2 ⇒ C 2 ; 0 ; 2
C ' D ' → = C D → = − 1 ; − 1 ; − 1 ⇒ x D ' = − 1 + 4 = 3 y D ' = − 1 + 5 = 4 z D ' = − 1 − 5 = − 6 ⇒ D ' 3 ; 4 ; − 6
Cách 2: Do A B C D . A ' B ' C ' D ' là hình hộp nên ta có ABCD là hình bình hành.
Suy ra
O A → + O C → = O B → + O D → ⇒ O C → = O B → + O D → − O A → ⇒ C = 2 ; 0 ; 2
Tương tự ta có:
O C → + O D ' → = O D → + O C ' → ⇒ O D ' → = O D → + O C ' → − O C → ⇒ D ' = 3 ; 4 ; − 6

Gọi I là tâm của hình vuông thì I chính là hình chiếu của C lên BD
Ta có: I ( -1+4t;1-t;-1+t )nên C I → = 4 t - 2 ; 2 - t ; t + 1
Vì C I ⊥ B D nên
C I ⇀ . u B D → = 0 ⇔ 4 4 t - 2 - 2 - t + t + 1 = 0 ⇔ t = 1 2
Do đó: I 1 ; 1 2 ; - 1 2 , C I - 3 2 2
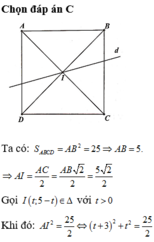
I là trung điểm AC ⇒ A ( 1;2;3 )
Tọa độ điểm B - 1 + 4 t ; 1 - t ; - 1 + t với t > 1 4
Ta có IB = IC nên
- 2 + 4 t 2 + 1 2 - t 2 + 1 2 + t 2 = 9 2 ⇔ t 2 - t = 0 ⇔ t = 0 t = 1
Tọa độ điểm B ( 3;0;0 ). Suy ra d ( -1;1;-1 )
Đáp án D

Chọn D.
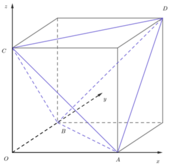
Phương pháp: Tứ diện ABCD có các cặp cạnh đối diện bằng nhau là tứ diện gần đều.
Cách giải: Theo giả thiết suy ra:
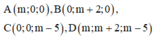
Theo tính chất của tứ diện gần đều tâm mặt cầu ngoại tiếp I của tứ diện ABCD là trung điểm OD
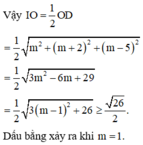
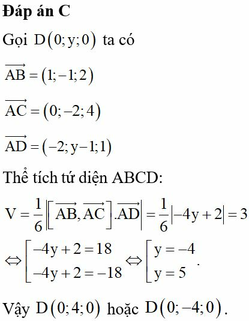
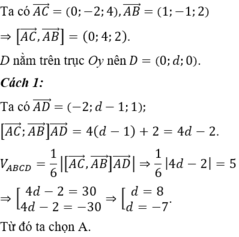




pn ghj the aj hju
-1 1 2 3 1 2 3 -1 -2 -3 -2 -3 A B C D