Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) B A H ^ + M A C ^ vì cùng phụ với A B C ^
b) A 1 ^ = C 1 ^ (1) (chứng minh a)
Mà DABC vuông có AM là trung tuyến nên DAMC cân tại M C 1 ^ = A 4 ^ (2).
Từ (1) và (2) suy ra A 1 ^ = A 4 ^ (3)
D thuộc đường trung trực của BC.
Þ DM ^ BC = {M}
Þ D 1 ^ = A 2 ^
Vì DM = MA (giả thiết) ⇒ M 1 ^ = A 3 ^ ⇒ A 2 ^ = A 3 ^ (4)
Từ (3) và (4) Þ AD là phân giác chung của M A H ^ & C A B ^
c) Theo cách vẽ và kết quả câu b), ta có AEDF là hình vuông.
d) DDBE = DDCF (cạnh huyền - cạnh góc vuông)
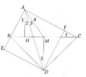

a) Ta có: ^BAH = ^BCA (vì 2 góc này cùng phụ với ^B)
Mà: ^MAC = ^BCA (tg MAC cân tại M vì Tg ABC vuông tại A có AM là trung tuyến)
Nên: ^BAH = ^MAC (4)
b) Tg AMD cân tại M (vì MA=MD) => ^D = ^DAM (1)
Ta có: MD//AH ( vì MD_I_ HM, AH _I_ HM )
Nên: ^D = ^DAH (2)
(1)(2) => ^DAM = ^DAH (3) => AD là p/g của ^HAM (5)
(3)(4) => ^BAH + ^DAH = ^MAC + ^DAM <=> ^BAD=^CAD => AD là p/g của ^BAC (6)
(5)(6) => AD là p/g chung của ^HAM và ^BAC
c) Ta có: AEDF là hcn ( vì ^E=^F=^A=90o )
Mà: AD là p/g của ^EAC (cmt)
Nên: AEDF là hình vuông
d) Tg DBE (^DEA=90o) và tg DCF (^DFC=90o) có:
DE = DF (AEDF là hình vuông)
DB = DC (MD là đường trung trực của BC)
Nên: Tg DBE = tg DCF (ch-cgv)

a: góc MAC=góc C
góc C=góc BAH
Do đó: góc MAC=góc BAH
c: Xét tứ giác AEDF có
góc AED=góc AFD=góc FAE=90 độ
AD là phân giác của góc FAE
Do đó: AEDF là hình vuông

a)Ta có
BK=KC (GT)
AK=KD( Đối xứng)
suy ra tứ giác ABDC là hình bình hành (1)
mà góc A = 90 độ (2)
từ 1 và 2 suy ra tứ giác ABDC là hình chữ nhật
b) ta có
BI=IA
EI=IK
suy ra tứ giác AKBE là hình bình hành (1)
ta lại có
BC=AD ( tứ giác ABDC là hình chữ nhật)
mà BK=KC
AK=KD
suy ra BK=AK (2)
Từ 1 và 2 suy ra tứ giác AKBE là hình thoi
c) ta có
BI=IA
BK=KC
suy ra IK là đường trung bình
suy ra IK//AC
IK=1/2AC
mà IK=1/2EK
Suy ra EK//AC
EK=AC
Suy ra tứ giác AKBE là hình bình hành
B A C D E K

a)Xét tứ giác ABDC :
AM = MD ; BM = MC
=>Tứ giác ABDC là hình bình hành
Mà góc BAC = 90 = >Tứ giác ABDC là hcn
b)Xét tam giác AID :
AH= HI ; AM = MD (gt)
=> HM song song ID ( đường tb)
=>tứ giác BIDC la ht
AC la trung truc AI = > tam giac ABI can tai B
=> AB = BI ma AB = DC ( ABDC la hcn )=> BI = DC
hay BIDC la hinh thang can
c) Ta có góc ACB = góc AHM = góc AEF
góc BAM = góc ABM
mà góc ABM + góc ACM = 90 => góc AEF + góc BAM = 90 độ hay AM vuông góc EF ( đccm)
a) Ta có: ^BAH = ^BCA (vì 2 góc này cùng phụ với ^B)
Mà: ^MAC = ^BCA (tg MAC cân tại M vì Tg ABC vuông tại A có AM là trung tuyến)
Nên: ^BAH = ^MAC (4)
b) Tg AMD cân tại M (vì MA=MD) => ^D = ^DAM (1)
Ta có: MD//AH ( vì MD_I_ HM, AH _I_ HM )
Nên: ^D = ^DAH (2)
(1)(2) => ^DAM = ^DAH (3) => AD là p/g của ^HAM (5)
(3)(4) => ^BAH + ^DAH = ^MAC + ^DAM <=> ^BAD=^CAD => AD là p/g của ^BAC (6)
(5)(6) => AD là p/g chung của ^HAM và ^BAC
c) Ta có: AEDF là hcn ( vì ^E=^F=^A=90o )
Mà: AD là p/g của ^EAC (cmt)
Nên: AEDF là hình vuông
d) Tg DBE (^DEA=90o) và tg DCF (^DFC=90o) có:
DE = DF (AEDF là hình vuông)
DB = DC (MD là đường trung trực của BC)
Nên: Tg DBE = tg DCF (ch-cgv)
bạn vẽ hình kiểu j thế?????