Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(\angle BEC=\angle BDC=90\Rightarrow BCDE\) nội tiếp
Gọi I là trung điểm BC
Vì \(\Delta BEC\) vuông tại E có I là trung điểm BC \(\Rightarrow IE=IB=IC\)
Vì \(\Delta BDC\) vuông tại D có I là trung điểm BC \(\Rightarrow ID=IB=IC\)
\(\Rightarrow ID=IE=IB=IC\Rightarrow I\) là tâm của (BCDE)
b) Vì AK là đường kính \(\Rightarrow\angle ABK=\angle ACK=90\)
\(\Rightarrow\left\{{}\begin{matrix}BK\bot AB\\CK\bot AC\end{matrix}\right.\) mà \(\left\{{}\begin{matrix}CH\bot AB\\BH\bot AC\end{matrix}\right.\Rightarrow\) \(CH\parallel BK,BH\parallel CK\)
\(\Rightarrow BHCK\) là hình bình hành có I là trung điểm BC
\(\Rightarrow H,I,K\) thẳng hàng

a)Gọi I là trung điểm của tam giác BC
Áp dụng đường trung tuyến cạnh huyền của tam giác EBC và DBC
=>IE=ID=IB=IC
=> tứ giác BCDE nội tiếp. tâm đường tròn là I
b)AFK=90 ( dg cao thứ 3)
ACK=90 (chắn nữa dg tròn)
=>AFB=ACK
c)BD vg góc với AC
ACK=90 =>CK vg góc với AC
=>CK song song với BH
tuong tu CH song song voi BK
=>BHCK là hinh binh hanh
*vì I là trung điểm của BC
=>I cung la trung diem cua HK
=>H,I,K thang hang

a: Xét (O) có
ΔABK nội tiếp
AK là đường kính
Do đó: ΔABK vuông tại B
=>BK vuông góc với AB
=>BK//CH
Xét (O) có
ΔACK nội tiếp
AK là đường kính
Do đó: ΔACK vuông tại C
=>AC vuông góc với CK
=>CK//BH
Xét tứ giác BHCK có
BH//CK
BK//CH
Do đó: BHCK là hình bình hành
b: Vì BHCK là hình bình hành
nên BC cắt HK tại trung điểm của mỗi đường
=>M là trung điểm của HK
Xét ΔKAH có
KO/KA=KM/KH
nên OM//AH và OM/AH=KO/KA=1/2
=>OM=1/2AH

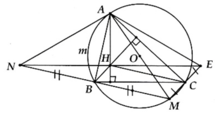
Cho △ABC nhọn (AB<AC) nội tiếp (O), 2 đường cao BD và CE cắt nhau tại H
a/ Chứng minh : B,C,D,E cùng nằm trên một đường tròn .Xác định tâm M của đường tròn này.
b/ Chứng minh : OM // AH
c/ Chứng minh : AB.AE = AC.AD
d/ Gọi K là điểm đối xứng của H qua M .

a, BH ^ AC và CM ^ AC Þ BH//CM
Tương tự => CH//BM
=> BHCM là hình bình hành
b, Chứng minh BNHC là hình bình hành
=> NH//BC
=> AH ^ NH => A H M ^ = 90 0
Mà A B N ^ = 90 0 => Tứ giác AHBN nội tiếp
c, Tương tự ý b, ta có: BHEC là hình bình hành. Vậy NH và HE//BC => N, H, E thẳng hàng
d, A B N ^ = 90 0 => AN là đường kính đường tròn ngoại tiếp tứ giác AHBN
AN = AM = 2R, AB = R 3 => A m B ⏜ = 120 0
S A O B = 1 2 S A B M = R 2 3 4
S A m B ⏜ = S a t A O B - S A O B = R 2 12 4 π - 3 3
=> S cần tìm = 2 S A m B ⏜ = R 2 6 4 π - 3 3

ta có
\(\widehat{AEH}=90^0;\widehat{AFH}=90^0\)
=> \(\widehat{AEH}+\widehat{AFH}=180^0\)
=> tứ giác AEHF nội tiếp được nhé
ta lại có AEB=ADB=90 độ
=> E , D cùng nhìn cạnh AB dưới 1 góc zuông
=> tứ giác AEDB nội tiếp được nha
b)ta có góc ACK = 90 độ ( góc nội tiếp chắn nửa đường tròn)
hai tam giác zuông ADB zà ACK có
ABD = AKC ( góc nội tiếp chắn cung AC )
=> tam giác ABD ~ tam giác AKC (g.g)
c) zẽ tiếp tuyến xy tại C của (O)
ta có OC \(\perp\) Cx (1)
=> góc ABC = góc DEC
mà góc ABC = góc ACx
nên góc ACx= góc DEC
do đó Cx//DE ( 2)
từ 1 zà 2 suy ra \(OC\perp DE\)

a: Xét (O) có
ΔABK nội tiếp đường tròn
AK là đường kính
Do đó: ΔABK vuông tại B
Xét (O) có
ΔACK nội tiếp đường tròn
AK là đường kính
Do đó: ΔACK vuông tại C
Xét tứ giác BHCK có
BH//CK
BK//CH
Do đó: BHCK là hình bình hành