Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

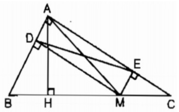
Ta có: AH ⊥ BC nên AM ≥ AH (quan hệ đường vuông góc và đường xiên)
Dấu “=” xảy ra khi M trùng với H
Mà DE = AM ( chứng minh trên)
Vậy DE có độ dài nhỏ nhất bằng AH khi M là chân đường vuông góc kẻ từ A đến BC

Em tham khảo tại link dưới đây nhé:
Câu hỏi của Trần Thị Vân Ngọc - Toán lớp 8 - Học toán với OnlineMath
hihihihihihiihiihiihihiihihihihihihihihihihihihihihiihihiihihihihihihiihihihihihihihihihihihihihihihihhihihihihihihihhiihihihihihiihihiihihihihihihihihihihihihihihihihiihihihihihiihihihihihihihihihiihihihihiihiihihihihiihihihihihiihihihihihiihhiihihihiihihihihihiihihihihhiihhiihiihihihihihihihihihihihiihhiiihhiihhiihihihihihihihiihihih

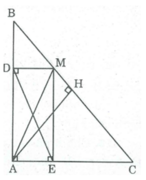
Gọi H là trung điểm của BC
Suy ra: AH ⊥ BC (tính chất tam giác cân)
Do đó, AM ≥ AH ( quan hệ đường vuông góc và đường xiên )(dấu " = " xảy ra khi M trùng với H)
Tứ giác ADME là hình chữ nhật .
⇒ AM = DE (tính chất hình chữ nhật)
Suy ra: DE ≥ AH
Vậy DE có độ dài nhỏ nhất là AH khi và chỉ khi điểm M là trung điểm của BC.


Ta có \(DE=AM\ge AH\). Dấu " = " xảy ra khi \(M\equiv H\)
Vậy DE có độ dài nhỏ nhất là AH khi điểm M là trung điểm của BC.

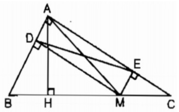
Xét tứ giác ADME, ta có:
∠ A = 90 0 (gt)
MD ⊥ AB (gt)
⇒ ∠ (MDA ) = 90 0
ME ⊥ AC (gt)
⇒ ∠ (MEA ) = 90 0
Suy ra tứ giác ADME là hình chữ nhật ( vì có ba góc vuông)
⇒ AM = DE ( tính chất hình chữ nhật)
Em tham khảo tại link dưới đây nhé:
Câu hỏi của Trần Thị Vân Ngọc - Toán lớp 8 - Học toán với OnlineMath