
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
góc BAH + góc HAC= 90độ (tam giác ABC vuông tại H)
Mà góc BAH + góc ABH =90độ (tam giác ABH vuông tại H)
=>góc ABH= góc HAC
Vậy góc B = góc HAC
A B C H K
cái tam giác mik vẽ là tam giác vuông cân nên góc B = góc C
nếu là tam giác thường thì khi đó:
kẻ đường thẳng sog song với AB đí qua H cắt AC tại K ( theo hibhf vẽ)
khi đó theo tính chất 2 đường thẳng song song sẽ có HK // BA
mà BA vuông góc tại AC( tam giác ABC vuông tại A)
=> HK vuông góc với AC
theo tính chất đồng vị => góc B = góc CHK

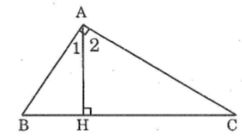
Có thể tìm góc B bằng hai cách:
Cách 1
Ta có: ∠(A1 ) + ∠(A2 ) = ∠(BAC) = 90o(1)
Vì ΔAHB vuông tại H nên:
∠B + ∠(A1) = 90o(tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra ∠B = ∠(A2 )
Cách 2
Vì ΔABC vuông tại A nên:
∠B +∠C = 90o (theo tính chất tam giác vuông) (1)
Vì ΔAHC vuông tại H nên:
∠(A2 ) + ∠C = 90o (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: ∠B = ∠(A2)


Có thể tìm góc B bằng hai cách:
Cách 1
Ta có: ∠(A1 ) + ∠(A2 ) = ∠(BAC) = 90o(1)
Vì ΔAHB vuông tại H nên:
∠B + ∠(A1) = 90o(tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra ∠B = ∠(A2 )
Cách 2
Vì ΔABC vuông tại A nên:
∠B +∠C = 90o (theo tính chất tam giác vuông) (1)
Vì ΔAHC vuông tại H nên:
∠(A2 ) + ∠C = 90o (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: ∠B = ∠(A2)

a) Sửa đề: Trên HC lấy E sao cho HE=HB và c/m ΔBHA=ΔEHA
Xét ΔBHA vuông tại H và ΔEHA vuông tại H có
AH chung
BH=EH(gt)
Do đó: ΔBHA=ΔEHA(hai cạnh góc vuông)
Hình tự vẽ
Xét tam giác ABC có \(\widehat{A}=90^o=>\widehat{B}+\widehat{C}=90^o\)
Xét tam giác HAC có \(\widehat{AHC}=90^o=>\widehat{C}+\widehat{HAC}=90^o\)
Từ 2 điều trên => \(\widehat{B}=\widehat{HAC}\)