Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

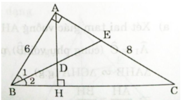
a) Ta có BE là phân giác của ∠ABC (gt)
⇒ ∠B1 = ∠B2
Do đó hai tam giác vuông:
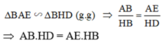
b) Ta có:
![]()
(định lý Pitago)
Xét hai tam giác vuông AHB và CAB có góc B chung nên :
![]()
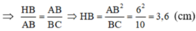
![]()


A B C E H D 1 2
Xét △ ABE và △ HBD có
\(\widehat{D}=\widehat{A}\left(=90^0\right)\)
\(\widehat{B1}=\widehat{B2}\)(gt)
=> △ ABE ∼ △ HBD (g.g)
=> \(\dfrac{AB}{HB}=\dfrac{AE}{HD}\)
=> AB.HD =AE.HB(đpcm)
b) Xét △ ABC có \(\widehat{A}=90^0\) theo đl py ta go ta có
BC2=AB2+AC2
⇔ BC2=62+82
⇔ BC2 = 100
⇔ BC =10
VÌ BD là pg của \(\widehat{ABC}\)
=> \(\dfrac{AB}{AE}=\dfrac{BC}{CE}\)
đặt AE là x ta có
=> \(\dfrac{6}{x}=\dfrac{10}{8-x}\)
=> 10x =6(8-x)
⇔ 10x=48-6x
⇔ 10x+6x=48
⇔ 16x=48
⇔x=3
=> AE =3(cm)
vì △ ABE ∼ △ HBD (theo a)
=> \(\dfrac{AB}{HB}=\dfrac{AE}{HD}\)
=> \(\dfrac{HD}{HB}=\dfrac{AE}{AB}=\dfrac{3}{6}=\dfrac{1}{2}\)
=> \(\dfrac{S_{\Delta ABE}}{S_{\Delta HBD}}=\left(\dfrac{1}{2}\right)^2=\dfrac{1}{4}\)

Xét tam giacs ABE và HBD ta có:
Góc BAE = Góc BHD (=90^0)
Góc ABE = Góc HBD (GT)
=> Tam giacs ABE đồng dạng với tam giác HBD
\(\Rightarrow\dfrac{AB}{HB}=\dfrac{AE}{HD}\)
=> AB.HD = AE.HB
a) Xét 2 Δ ABE và Δ HBD có :
góc ABE = góc HBD ( vì BE là p/g góc B)
góc A = góc H (=900)
=> ΔABE đồng dạng vs ΔHBD
=> AB/AE= HB/HD=> AB.HD= AE.HB( đpcm)
Làm tiếp phần b nữa đi bạn