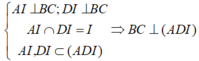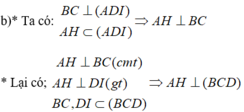Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do \(d\perp\left(ABC\right)\) nên \(MN\perp BC\)
\(\left\{{}\begin{matrix}MC\perp\left(BOH\right)\\BN\subset\left(BOH\right)\end{matrix}\right.\) \(\Rightarrow MC\perp BN\)
\(\left\{{}\begin{matrix}MB\perp\left(CHO\right)\\CN\subset\left(CHO\right)\end{matrix}\right.\)\(\Rightarrow MB\perp CN\)

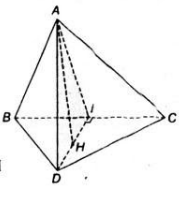
SA vuông góc với (ABC)=> SA vuông góc với BC
mà AB vuông góc với BC ( tam giác ABC vuông)
=> BC vg góc với (SAB)=> BC vg góc AH
mà AH vg góc SB
=> AH vg góc (SBC)=> AH vg góc SC

TenAnh1 TenAnh1 A = (-0.14, -7.4) A = (-0.14, -7.4) A = (-0.14, -7.4) B = (14.46, -7.36) B = (14.46, -7.36) B = (14.46, -7.36) C = (-3.74, -5.6) C = (-3.74, -5.6) C = (-3.74, -5.6) D = (11.62, -5.6) D = (11.62, -5.6) D = (11.62, -5.6) E = (-3.34, -5.86) E = (-3.34, -5.86) E = (-3.34, -5.86) F = (12.02, -5.86) F = (12.02, -5.86) F = (12.02, -5.86) G = (-3.7, -5.88) G = (-3.7, -5.88) G = (-3.7, -5.88) H = (11.66, -5.88) H = (11.66, -5.88) H = (11.66, -5.88) I = (-3.74, -5.62) I = (-3.74, -5.62) I = (-3.74, -5.62) J = (11.62, -5.62) J = (11.62, -5.62) J = (11.62, -5.62) A'

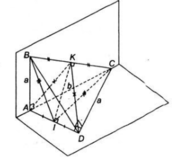


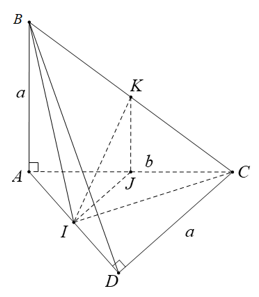
Chứng minh tương tự, ta có tam giác AKD là tam giác cân tại K có KI là đường trung tuyến nên đồng thời là đường cao.
⇒ IK ⊥ AD (2)
Từ (1) và (2) suy ra; IK là đường vuông góc chung của hai đường thẳng AD và BC.

+) MN là đường trung trung bình của tam giác BCD nên MN // CD mà CD \(\bot\) BC suy ra MN \(\bot BC \) (1)
+) tam giác ABC cân tạ A nên AM vùa là đường trung tuyến vùa là đường cao suy ra AM \(\bot\)BC (2)
Từ (1)(2) suy ra BC\(\bot\)(AMN) suy ra (ABC) \(\bot\)(AMN)

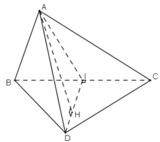
a) Tam giác ABC cân tại A có AI là đường trung tuyến nên đồng thời là đường cao:
AI ⊥ BC
+) Tương tự, tam giác BCD cân tại D có DI là đường trung tuyến nên đồng thời là đường cao:
DI ⊥ BC
+) Ta có: