Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hệ thức lượng: \(AH^2=BH.CH\)
Hai tam giác vuông BEH và HFC đồng dạng: \(\Rightarrow\dfrac{BE}{FH}=\dfrac{EH}{CF}\Rightarrow BE.CF=EH.FH\)
Hai tam giác vuông AEH và CFH đồng dạng \(\Rightarrow\dfrac{AH}{CH}=\dfrac{EH}{FH}\Rightarrow AH.FH-CH.EH=0\)
Hai tam giác vuông BEH và AFH đồng dạng \(\Rightarrow\dfrac{BH}{AH}=\dfrac{EH}{FH}\Rightarrow EH.AH-BH.FH=0\)
Ta có: \(\left(BE\sqrt{CH}+CF\sqrt{BH}\right)^2=BE^2.CH+CF^2.BH+2BE.CF.\sqrt{BH.CH}\)
\(=BE^2.CH+CF^2.BH+2BE.CF.AH\)
\(=\left(BH^2-EH^2\right)CH+\left(CH^2-FH^2\right)BH+2BE.CF.AH\)
\(=BH.CH\left(BH+CH\right)-EH^2.CH-FH^2.BH+2EH.FH.AH\)
\(=AH^2.BC+EH\left(AH.FH-EH.CH\right)+FH\left(AH.EH-FH.BH\right)\)
\(=AH^2.BC=\left(AH\sqrt{BC}\right)^2\)
\(\Rightarrow BE\sqrt{CH}+CF\sqrt{BH}=AH\sqrt{BC}\)

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=10^2-6^2=64\)
=>AC=8(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\AB^2=BH\cdot BC\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AH=\dfrac{6\cdot8}{10}=4,8\left(cm\right)\\BH=\dfrac{6^2}{10}=3,6\left(cm\right)\end{matrix}\right.\)
b: ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra AE*AB=AF*AC
=>AE/AC=AF/AB
Xét ΔAEF vuông tại A và ΔACB vuông tại A có
AE/AC=AF/AB
Do đó: ΔAEF đồng dạng với ΔACB
c: Xét ΔBAC có BD là phân giác
nên \(\dfrac{AD}{AB}=\dfrac{CD}{CB}\)
=>\(\dfrac{AB}{AD}=\dfrac{CB}{CD}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AB}{AD}=\dfrac{CB}{CD}=\dfrac{AB+BC}{AD+CD}=\dfrac{AB+BC}{AC}\)(1)
ΔBAD vuông tại A có
\(cotABD=\dfrac{AB}{AD}\)(2)
BD là phân giác của góc ABC
=>\(\widehat{ABD}=\widehat{DBC}\left(3\right)\)
Từ (1),(2),(3) suy ra \(cotDBC=\dfrac{AB+BC}{AC}\)

Lời giải:
Áp dụng hệ thức lượng trong tam giác vuông đối với tam giác vuông $AHB$, đường cao $HE$:
$EA.EB=HE^2$
Tương tự: $FA.FC=HF^2$
$\Rightarrow EA.EB+FA.FC=HE^2+HF^2=EF^2(1)$ (định lý Pitago)
Mặt khác: Dễ thấy $HEAF$ là hình chữ nhật do có 3 góc $\widehat{E}=\widehat{A}=\widehat{F}=90^0$
$\Rightarrow EF=HA$
$\Rightarrow EF^2=HA^2(2)$
Áp dụng hệ thức lượng trong tam giác vuông $ABC$:
$AH^2=HB.HC(3)$
Từ $(1);(2); (3)\Rightarrow EA.EB+FA.FC=HB.HC$ (đpcm)

a: CH=6cm
\(AB=\sqrt{BH\cdot BC}=4\left(cm\right)\)
\(\widehat{C}=30^0\)

Bạn tự vẽ hình.
(a) \(BC^2=AB^2+AC^2\left(Pythagoras\right)\)
\(\Rightarrow AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-3^2}=4\left(cm\right)\)
+) \(sinB=\dfrac{AC}{BC}=\dfrac{4}{5}\Rightarrow\hat{B}\approx53^o\)
+) \(\hat{C}=90^o-\hat{B}\approx90^o-53^o=37^o\)
(b) +) \(AB.AC=BC.AH\Leftrightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{3\cdot4}{5}=2,4\left(cm\right)\)
\(\hat{A}=\hat{E}=\hat{F}=90^o\left(gt\right)\Rightarrow AEHF\) là hình chữ nhật.
Do đó, \(EF=AH\left(đpcm\right)\)

Lời giải:
a. Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10$ (cm)
$AH=2S_{ABC}:BC=AB.AC:BC=6.8:10=4,8$ (cm)
$\sin B = \frac{AC}{BC}=\frac{8}{10}=\frac{4}{5}$
b.
Áp dụng hệ thức lượng trong tam giác vuông ta có:
$BE.BA=BH^2$
$AF.AC=AH^2$
$\Rightarrow BE.BA+AF.AC=BH^2+AH^2=AB^2$ (đpcm)

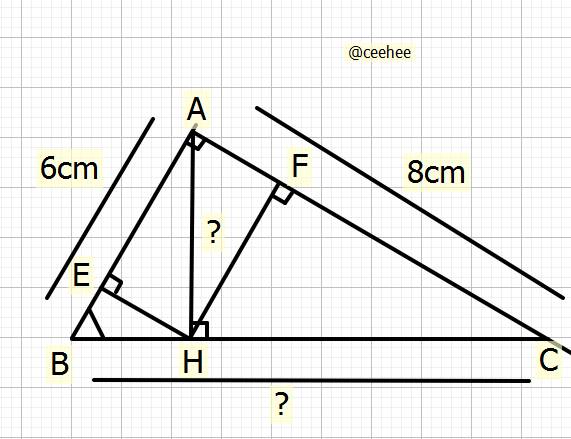
`a)` Tỉ số lượng giác góc `B` của \(\Delta ABC\)
\(SinB=\dfrac{AC}{BC}\\ CosB=\dfrac{AB}{BC}\\ TanB=\dfrac{AC}{AB}\\ CotB=\dfrac{AB}{AC}\)
`b)` Tính `BC,AH`
Xét \(\Delta ABC\) vuông tại `A`, đường cao `AH`
Ta có: \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\left(htl\right)\)
\(\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{6^2}+\dfrac{1}{8^2}\\ \Rightarrow\dfrac{1}{AH^2}=\dfrac{25}{576}\\ \Rightarrow AH^2=\dfrac{576\cdot1}{25}=23,04\\ \Rightarrow AH=\sqrt{23,04}=4,8cm\)
Ta có: \(AB\cdot AC=AH\cdot BC\left(htl\right)\)
\(\Rightarrow6\cdot8=4,8\cdot BC\\ \Rightarrow48=4,8\cdot BC\\ \Rightarrow BC=\dfrac{48}{4,8}\\ \Rightarrow BC=10cm\)
Vậy: `AH = 4,8cm; BC= 10cm`
`c)` C/m: `AE * AB = AF * AC`
Xét \(\Delta AHB\) vuông tại `H`, đường cao `HE`
Ta có: \(AH^2=AE\cdot AB\left(htl\right)\) `(1)`
Xét \(\Delta AHC\) vuông tại `H`, đường cao `HF`
Ta có: \(AH^2=AF\cdot AC\left(htl\right)\) `(2)`
Từ `(1)` và `(2)` \(\Rightarrow AH^2=AH^2\)
\(\Rightarrow AE\cdot AB=AF\cdot AC\left(=AH^2\right).\)
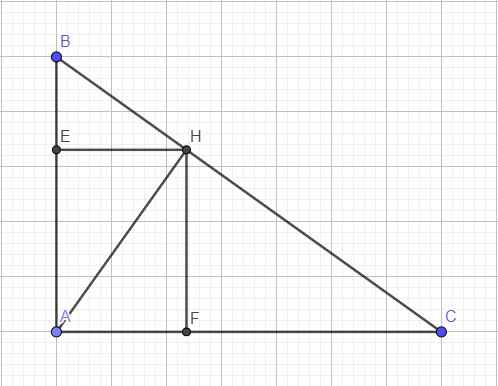
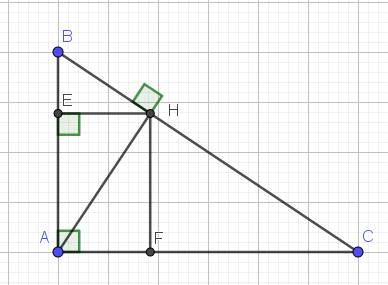
\(a,\) Áp dụng HTL tam giác
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AH^2=BH\cdot HC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BC=\dfrac{AB^2}{BH}=\dfrac{3600}{36}=100\left(cm\right)\\AH=\sqrt{36\left(100-36\right)}=\sqrt{36\cdot64}=6\cdot8=48\left(cm\right)\end{matrix}\right.\)
\(AC=\sqrt{BC^2-AB^2}=80\left(cm\right)\left(pytago\right)\)
\(b,\) Áp dụng HTL trong tam giác ABC,AHB và AHC, ta có
\(\left\{{}\begin{matrix}AB\cdot AC=AH\cdot BC\\BH^2=AB\cdot BE\\CH^2=AC\cdot CF\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BC=\dfrac{AB\cdot AC}{AH}\\BE=\dfrac{BH^2}{AB}\\CF=\dfrac{CH^2}{AC}\end{matrix}\right.\)
\(\Rightarrow BE\cdot CF=\dfrac{\left(BH\cdot CH\right)^2}{AB\cdot AC}=\dfrac{AH^4}{AB\cdot AC}\left(AH^2=BH\cdot HC\right)\\ \Rightarrow BE\cdot CF\cdot BC=\dfrac{AB\cdot AC}{AH}\cdot\dfrac{AH^4}{AB\cdot AC}=AH^3\left(Đpcm\right)\)