
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì tam giác ABC vuông nên ta có:
\(\text{cosB=sinC=0,8}\)
\(\text{cosC=}\)\(\sqrt{1-sin^2C}\) (theo công thức trong SGK ^^)=\(\sqrt{1-0,8^2}=0,6\)
\(tangC=\dfrac{sinC}{cosC}=\dfrac{0,8}{0,6}=\dfrac{4}{3}\left(\approx1,3\right)\)
\(cotangC=\dfrac{cosC}{sinC}=\dfrac{0,6}{0,8}=0,75\)

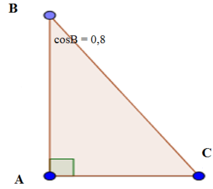
Ta có: ∠B + ∠C = 90o nên sinC = cosB = 0,8
Từ công thức sin2C + cos2C = 1 ta suy ra:
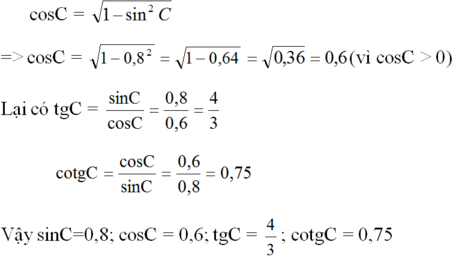

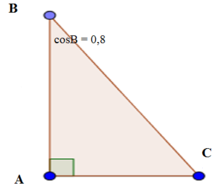
Ta có: ∠B + ∠C = 90o nên sinC = cosB = 0,8
Từ công thức sin2C + cos2C = 1 ta suy ra:
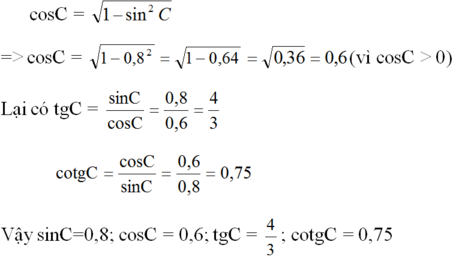

cosB=0,8=4/5 => BA=4 , BC=5
Áp dụng định lý Pytago trong tam giác vuông ABC, có:
AC2=BC2-BA2
(=) AC2=52-42=9
(=) AC=3
Ta có:
sinC=BA/BC=4/5
cosC=AC/BC=3/5
tanC=BA/AC=4/3
cotC=AC/BA=3/4
\(sin^2B+cos^2B=1\Leftrightarrow sin^2B-1-\left(0,8\right)^2=0.36.\Leftrightarrow sinB=0,6.\\\)
\(tanB=\frac{sinB}{cosB}=\frac{0,6}{0,8}=\frac{3}{4}\)
\(cotB=\frac{1}{tanB}=\frac{1}{\frac{3}{4}}=\frac{4}{3}.\)

Ta có:
\(cosB=\dfrac{AB}{BC}\Rightarrow AB=BC.cosB=10.0,8=8\left(cm\right)\)
\(AC=\sqrt{BC^2-AB^2}=6\left(cm\right)\)
b.
\(sinC=\dfrac{AB}{BC}=\dfrac{8}{10}=0,8\)
\(cosC=\dfrac{AC}{BC}=\dfrac{6}{10}=0,6\)
\(tanC=\dfrac{AB}{AC}=\dfrac{8}{6}=\dfrac{4}{3}\)
\(cotC=\dfrac{AC}{AB}=\dfrac{3}{4}\)


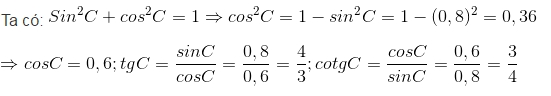
Vì tam giác ABC vuông tại A nên góc C nhọn. Vì thế:
sinC>0;cosC>0;tanC>0;cotC>0sinC>0;cosC>0;tanC>0;cotC>0
Vì hai góc B và C phụ nhau nên sinC = cosB = 0,8.
Ta có:
Sin2C+cos2C=1Sin2C+cos2C=1
⇒cos2C=1−sin2C=1−(0,8)2=0,36⇒cos2C=1−sin2C=1−(0,8)2=0,36
⇒cosC=0,6;⇒cosC=0,6;
tgC=sinCcosC=0,80,6=43;tgC=sinCcosC=0,80,6=43;
cotgC=cosCsinC=0,60,8=34