
Ta có:\(AC^2=HC^2+AH^2\)(Định lý pytago)
\(\Rightarrow AH^2=AC^2-HC^2=4^2-2^2=16-4=12\)
\(\Rightarrow AH=\sqrt{12}\approx3\)
Độ dài BC là :3+2=5
Chu vi của tam giác ABC la:\(4+5+5\approx14\)

Áp dụng định lý Pitago, ta có: \(AC^2=AH^2+HC^2\)
\(\Rightarrow20^2=12^2+HC^2\)
\(\Rightarrow HC^2=20^2-12^2\)
\(\Rightarrow HC^2=400-144=256\)
\(\Rightarrow HC=16\left(cm\right)\)
Áp dụng định lý Pitago, ta có: \(AB^2=BH^2+AH^2\)
\(\Rightarrow AB^2=5^2+12^2\)
\(\Rightarrow AB^2=25+144=169\)
\(\Rightarrow AB=13\left(cm\right)\)
Vậy CV tam giác ABC là
\(20+5+16+13=54\left(cm\right)\)

Trả lời :
Bạn vào câu hỏi tương tự hoặc lên mạng kham khải bài nhá.
# chúc bạn học tốt ạ #

A B C H
XÉT \(\Delta BAH\)VUÔNG TẠI H
CÓ \(AB^2=BH^2+HA^2\left(Đ/L,PY-TA-GO\right)\)
THAY\(5^2=BH^2+4^2\)
\(\Rightarrow BH^2=5^2-4^2\)
\(\Rightarrow BH^2=25-16\)
\(\Rightarrow BH^2=9\)
\(\Rightarrow BH=\sqrt{9}=3\left(cm\right)\)
TA CÓ \(BH+HC=BC\)
THAY\(3+12=BC\)
\(BC=15\left(cm\right)\)
XÉT \(\Delta HAC\)VUÔNG TẠI H
CÓ \(AC^2=AH^2+HC^2\)(Đ/L PYTAGO)
THAY\(AC^2=4^2+12^2\)
\(AC^2=16+144\)
\(AC^2=160\)
\(\Rightarrow AC=\sqrt{160}=4\sqrt{10}\)
CHU VI \(\Delta ABC\)LÀ
\(AB+AC+BC=5+4\sqrt{10}+15=20+4\sqrt{10}\)

A B H C
Xét \(\Delta\)AHC vuông tại H:
=> AC2 = HA2 + HC2
HC2 = AC2 - HA2
HC2 = 202 - 122 = 256
HC = \(\sqrt{256}\) = 16 (cm)
BC = BH + HC
BC = 5 + 16 = 21 (cm)
Xét \(\Delta\)AHB vuông tại H
=> AB2 = HA2 + HB2
AB2 = 122 + 52
AB2 = 144 + 25 = 169
AB = \(\sqrt{169}\) = 13 (cm)
Chu vi của \(\Delta\)ABC là:
AC + CB + BA = 20 + 21 + 13
= 54 (cm)
Vậy chu vi của \(\Delta\)ABC là 54 cm.
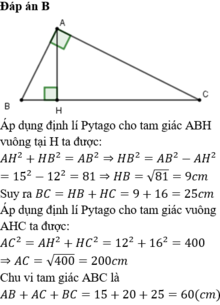

+ Xét \(\Delta ABH\) vuông tại \(H\left(gt\right)\) có:
\(AH^2+BH^2=AB^2\) (định lí Py - ta - go).
=> \(12^2+BH^2=15^2\)
=> \(BH^2=15^2-12^2\)
=> \(BH^2=225-144\)
=> \(BH^2=81\)
=> \(BH=9\left(cm\right)\) (vì \(BH>0\)).
+ Ta có: \(BH+CH=BC.\)
=> \(9+CH=24\)
=> \(CH=24-9\)
=> \(CH=15\left(cm\right).\)
+ Xét \(\Delta ACH\) vuông tại \(H\left(gt\right)\) có:
\(AC^2=AH^2+CH^2\) (định lí Py - ta - go).
=> \(AC^2=12^2+15^2\)
=> \(AC^2=144+225\)
=> \(AC^2=369\)
=> \(AC=\sqrt{369}\)
=> \(AC=3\sqrt{41}\left(cm\right)\) (vì \(AC>0\)).
=> Chu vi của tam giác \(ABC\) là:
\(AB+AC+BC=15+3\sqrt{41}+24\approx58,21\left(cm\right).\)
Vậy chu vi của tam giác \(ABC\) \(\approx58,21\left(cm\right).\)
Chúc bạn học tốt!
bn tự vẽ hình nhé
+ Xét ΔABHΔABH vuông tại H(gt)H(gt) có:
AH2+BH2=AB2AH2+BH2=AB2 (định lí Py - ta - go).
=> 122+BH2=152122+BH2=152
=> BH2=152−122BH2=152−122
=> BH2=225−144BH2=225−144
=> BH2=81BH2=81
=> BH=9(cm)BH=9(cm) (vì BH>0BH>0).
+ Ta có: BH+CH=BC.BH+CH=BC.
=> 9+CH=249+CH=24
=> CH=24
Đúng(0)