Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cho tam giác ABC vuông cân tại B.Trên cạnh BA và BC lấy hai điểm E và F sao cho BE = BF.Qua B và E kẻ đường vuông góc với AF,chúng cắt AC lần lượt ở I và K. EK cắt BC tại H
a)Chứng minh tam giác AHC cân
b)chứng minh I là trung điểm KC
c)Gọi M,N,P lần lượt là trung điểm EC,AF,EF

A B C H M N
a, Vì HM là đường cao => \(HM\perp AB\)=> ^HMA = 900
Vì HN là đường cao => \(HN\perp AC\)=> ^HNA = 900
Xét tứ giác AMHN có :
^HMA + ^HNA = 900
mà ^HMA ; ^HNA đối nhau
Vậy tứ giác AMHN nội tiếp
b, Xét tam giác ABH vuông tại H, đường cao HM ta có :
\(AH^2=AM.AB\)(1)
Xét tam giác ACH vuông tại H, đường cao HN ta có :
\(AH^2=AN.AC\)(2)
từ (1) ; (2) suy ra : \(AM.AB=AN.AC\Rightarrow\frac{AM}{AC}=\frac{AN}{AB}\)
Xét tam giác AMN và tam giác ACB ta có :
^A chung
\(\frac{AM}{AC}=\frac{AN}{AB}\)( cmt )
Vậy tam giác AMN ~ tam giác ACB ( c.g.c )

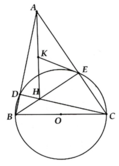
a, HS tự chứng minh
b, HS tự chứng minh
c, DAEH vuông nên ta có: KE = KA = 1 2 AH
=> DAKE cân tại K
=> K A E ^ = K E A ^
DEOC cân ở O => O C E ^ = O E C ^
H là trực tâm => AH ^ BC
Có A E K ^ + O E C ^ = H A C ^ + A C O ^ = 90 0
(K tâm ngoại tiếp) => OE ^ KE
d, HS tự làm
Mình chỉ giải đến câu c nha, câu d đang í ẹ chưa nghĩ ra
a, (O;R) có: \(\widehat{BMC}=\widehat{BNC}=90^o\)( góc nội tiếp chắn nửa đường tròn)
Tứ giác AMHN có: \(\widehat{AMH}+\widehat{ANH}=90^o+90^o=180^o\) nên tứ giác AMHN nội tiếp đường tròn có tâm là trung điểm của AH, đường kính AH
b, \(\Delta ABC\) có: BN, CM là đường cao, \(BN\cap CM=\left\{H\right\}\) nên H là trực tâm \(\Rightarrow AD\perp BC\)
Xét \(\Delta ADB\) và \(\Delta CMB\) có:
\(\widehat{ADB}=\widehat{CMB}=90^o\)
\(\widehat{BAD}=\widehat{BCM}\) (cùng phụ \(\widehat{MBC}\))
\(\Rightarrow\Delta ADB\sim\Delta CMB\left(g-g\right)\Rightarrow\frac{BD}{BA}=\frac{BM}{BC}\Leftrightarrow BD.BC=BM.BA\)c, \(\Delta ADC\) có: \(\widehat{ADC}=90^o\Rightarrow AC^2=AD^2+DC^2\) (định lý Py-ta-go) hay \(4a^2=AD^2+a^2\Leftrightarrow AD=a\sqrt{3}\)
\(\Delta ABC\) đều có AD, BN, CM là đường cao nên là trung tuyến
\(\Delta ABC\) đều có AD, BN, CM là trung tuyến, \(AD\cap BN\cap CM=\left\{H\right\}\) nên H là trọng tâm \(\Rightarrow AH=\frac{2}{3}AD\Leftrightarrow AH=\frac{2a\sqrt{3}}{3}\)
Gọi E là tâm đường tròn ngoại tiếp tứ giác AMHN \(\Rightarrow AE=EH=\frac{a\sqrt{3}}{3}\)
Chu vi đường tròn ngoại tiếp tứ giác AMHN là \(C=\frac{2a\sqrt{3}}{3}\pi\)