Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hơi khó nên tui dung tạm BĐT vậy , bạn thông cảm ^ ^
A B C H E F H
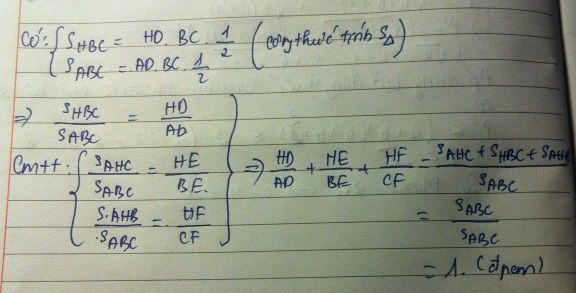
\(S\left(ABC\right)=AD.\frac{BC}{2}\)
\(S\left(BHC\right)=HD.\frac{BC}{2}\)
\(\Rightarrow\frac{HD}{AD}=\frac{S\left(BHC\right)}{S\left(ABC\right)}\left(1\right)\)
Tương tự:
\(\frac{HE}{BE}=\frac{S\left(AHC\right)}{S\left(ABC\right)}\left(2\right)\)
\(\frac{HF}{CF}=\frac{S\left(AHB\right)}{S\left(ABC\right)}\left(3\right)\)
(1) + (2) +(3) được:
\(\frac{HD}{AD}+\frac{HE}{BE}+\frac{HF}{CF}=\left[S\left(BHC\right)+S\left(AHC\right)+\frac{S\left(AHB\right)}{S\left(ABC\right)}\right]=\frac{S\left(ABC\right)}{S\left(ABC\right)}=1\)
Áp dụng bất đẳng thức: \(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\)9 ta có:
\(\left(\frac{HD}{AD}+\frac{HE}{BE}+\frac{HF}{CF}\right)\left(\frac{AD}{HD}+\frac{BE}{HE}+\frac{CF}{HF}\right)\ge9\)
mà: \(\frac{HD}{AD}+\frac{HE}{BE}+\frac{HF}{CF}=1\) \(\Rightarrow\left(\frac{AD}{HD}+\frac{BE}{HE}+\frac{CF}{HF}\right)\ge9\)

A B C F D E H
a,Ta có \(\frac{S_{HBC}}{S_{ABC}}=\frac{\frac{1}{2}HD.BC}{\frac{1}{2}AD.BC}=\frac{HD}{AD}\)
tương tự \(\frac{S_{HAC}}{S_{ABC}}=\frac{HE}{BE};\frac{S_{HAB}}{S_{ABC}}=\frac{HF}{CF}\)
\(\Rightarrow\frac{HD}{AD}+\frac{HE}{BE}+\frac{HF}{CF}=\frac{S_{HBC}}{S_{ABC}}+\frac{S_{HAC}}{S_{ABC}}+\frac{S_{HAB}}{S_{ABC}}=\frac{S_{HBC}+S_{HAC}+S_{HAB}}{S_{ABC}}=\frac{S_{ABC}}{S_{ABC}}=1\left(ĐPCM\right)\)
b, bổ sung đề rồi mình làm tiếp cho ạ
Câu b) em có cách này cô ạ, cô check giùm em xem có đúng không ạ :
Ta có : \(\frac{HA}{AD}=\frac{S_{ABH}}{S_{ABD}}=\frac{S_{AHC}}{S_{ADC}}=\frac{S_{ABH}+S_{AHC}}{S_{ABD}+S_{ADC}}=\frac{S_{ABH}+S_{AHC}}{S_{ABC}}\)
( Tính chất dãy tỉ số bằng nhau )
Tương tự ta có :
\(\frac{HB}{BE}=\frac{S_{AHB}+S_{BHC}}{S_{ABC}}\), \(\frac{HC}{CF}=\frac{S_{AHC}+S_{BHC}}{S_{ABC}}\)
Khi đó : \(\frac{HA}{AD}+\frac{HB}{BE}+\frac{HC}{CF}=\frac{2\left(S_{ABH}+S_{AHC}+S_{BHC}\right)}{S_{ABC}}=\frac{2S_{ABC}}{S_{ABC}}=2\)
Vậy : \(\frac{HA}{AD}+\frac{HB}{BE}+\frac{HC}{CF}=2\)
https://hoc24.vn/hoi-dap/question/954653.html
Tương tự nhé!
Bài này thì dễ mà đề nó nói không dùng BĐT mà
@Trần Quốc Khanh