Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

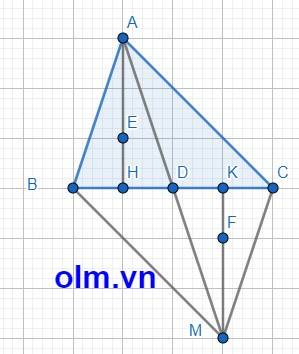
Xét tam giác ACD và tam giác MBD có:
AD = DM (gt)
BD = DC (gt)
\(\widehat{BDM}\) = \(\widehat{ADC}\) (hai góc đối đỉnh)
⇒ \(\Delta\)ACD = \(\Delta\) MBD (c-g-c)
Xét tứ giác ABMC có
AD = DM
BD = DC
⇒ tứ giác ABMC là hình bình hành vì tứ giác có hai đường chéo căt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành.
⇒ AC // BM
⇒ \(\widehat{ABM}\) = \(\widehat{MCA}\) (vì tứ giác ABMC là hình bình hành)
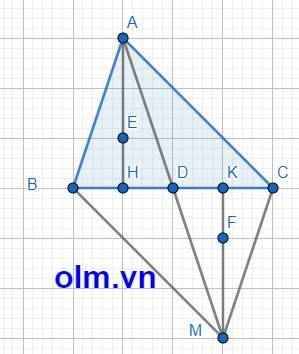
xét tam giác ACD và tam giác MBD có
AD=DM [ gt ]
BD=DC[ gt ]
BDM = ADC hai góc đối đỉnh
suy ra tam giác ACD= tam giác MBD [ c-g-c]
xét tứ giác ABMC có
AD = DM
BD=DC
suy ra tứ giác ABMC là hình bình hành vì tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành
suy ra ABM=MCA vì tứ giác ABMC là hình bình hành .

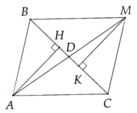
A B C M D
a) Xét ΔABD và ΔMCD có:
AD=MD(gt)
\(\widehat{ADB}=\widehat{CDM}\left(đđ\right)\)
BD=CD(gt)
=> ΔABD=ΔMCD(c.g.c)
b) Đính chính lại đề: CM AB vuông góc vs CM
VÌ: ΔABD=ΔMCD(cmt)
=> \(\widehat{ABD}=\widehat{MCD}\) . Mà hai góc này ở vị trí sole trong
=>AB//CM
c)Xét ΔBDM và ΔCDA có:
DB=DC(gt)
\(\widehat{BDM}=\widehat{CDA}\left(đđ\right)\)
DM=AD(gt)
=>ΔBDM=ΔCDA(c.g.c)
=>\(\widehat{BMD}=\widehat{CAD}\). Mà hai góc này ở vị trí sole trong
=>AC//BM
đọc nhầm đề lm lại từ phần b
b) Vì: ΔABD=ΔMCD(cmt)
=> \(\widehat{ABD}=\widehat{MCD}\) .Mà hai góc này ở vị trid sole trong
=> AB//CM
Mà: \(AB\perp AC\left(gt\right)\)
=> \(AC\perp CM\)
phần c vẫn như ở dưới

a/ Xét tg ADB và tg MDC có
AD=DM (gt) DB=DC (gt)
\(\widehat{ADB}=\widehat{MDC}\)(góc đối đỉnh)
=> tg ADB = tg MDC (c.g.c) => AC=BM
\(\Rightarrow\widehat{CAD}=\widehat{BMD}\)=> AC // BM (Hai đường thẳng bị cắt bởi đường thẳng thứ 3 tạo thành 2 góc so le trong = nhau thì chúng // với nhau)
b/
Xét tg ABM và tg MCA có
tg ABD = tg MCD (cmt) => AB = MC; AC = BM
AM chung
=> tg ABM = tg MCA (c.c.c)
c/
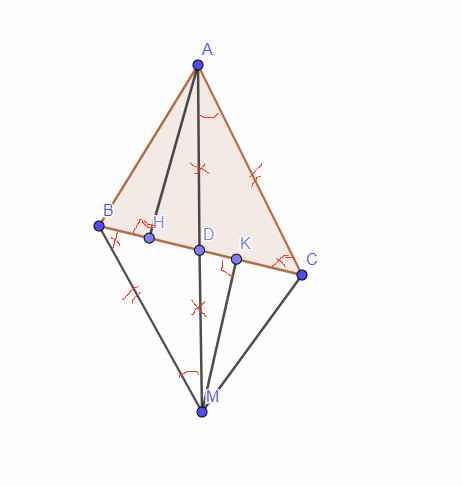
Xét tg vuông ABH và tg vuông MCK có
tg ABD = tg MCD (cmt) => \(\widehat{ABH}=\widehat{MCK}\)
AB=CM (cmt)
=> tg ABH = tg MCK (Hai tg vuông có cạnh huyền và góc nhọn tương ứng = nhau) => BH=CK
Mà BK=BC-CK; CH=BC-BH => BK=CH
d/
Xét tg vuông AHD và tg vuông MKD có
DA=DM (gt); \(\widehat{ADH}=\widehat{MDK}\)(góc đối đỉnh) => tg AHD = tg MKD (Hai tg vuông có cạnh huyền và góc nhọn tương ứng = nhau)
\(\Rightarrow\widehat{DAH}=\widehat{DMK}\) => HM // AK (Hai đường thẳng bị cắt bởi đường thẳng thứ 3 tạo thành 2 góc so le trong = nhau thì chúng // với nhau)

A B C D M H K
a,
*Xét tam giác BDM và tam giác CDA, ta có:
AD = MD (đề ra)
BD = CD (đề ra)
góc BDM = góc CDA (hai góc đối đỉnh)
=> tam giác BDM = tam giác CDA (c.g.c)
=> Góc CAD = góc BMD (hai góc tương ứng)
=> AC // BM (hai góc so le trong bằng nhau)
b,
cm trên.
c,
*Xét tam giác AHD và tam giác MKD, ta có:
AD = MD (đề ra)
Góc ADH = góc MDK (hai góc đối đỉnh)
=> Tam giác AHD = tam giác MKD (cạnh huyền góc nhọn)
=> HD = KD (hai cạnh tương ứng)
Ta có:
BK = BD + DK
CH = CD + HD
Mà BD = CD
HD = KD
=> BK = CH (đpcm)
d,
*Xét tam giác AKD và tam giác MHD, ta có:
AD = MD (đề ra)
HD = KD (cm trên)
Góc HDM = góc KDA (hai góc đối đỉnh)
=> Tam giác AKD = tam giác MHD (c.g.c)
=> Góc HMD = góc KAD (hai góc tương ứng)
=> HM // AK (hai góc so le trong bằng nhau)

A B C M
CM :
a) Áp dụng định lí Pi - ta - go vào t/giác ABC vuông tại A, ta có:
BC2 = AB2 + AC2
=> AB2 = BC2 - AC2 = 102 - 82 = 100 - 64 = 36
=> AB = 6 (cm)
b) Xét t/giác ABM và t/giác CDM
có: BM = MD (gt)
\(\widehat{AMB}=\widehat{CMD}\) (đối đỉnh)
AM = CM (gt)
=> t/giác ABM = t/giác CDM (c.g.c)
=> AB = CD (2 cạnh t/ứng)
=> \(\widehat{A}=\widehat{C}\) (2 góc t/ứng)
Mà \(\widehat{A}=90^0\) => \(\widehat{C}=90^0\) => AC \(\perp\)CD
c) Xét t/giác ACD
Ta có: BC + CD > BD (bất đẳng thức t/giác)
Mà CD = AB và 2BM = BD (vì BD = BM + MD và BM = MD)
=> AB + BC > 2BM
d) Ta có: AB < BC (6 cm < 10cm)
Mà AB = CD
=> CD > BC => \(\widehat{MBC}< \widehat{D}\) (quan hệ giữa cạnh và góc đối diện)
Mà \(\widehat{D}=\widehat{ABM}\) (vì t/giác ABM = t/giác CDM)
=> \(\widehat{CBM}< \widehat{ABM}\)
Cho tam giác ABC vuông tại A có AB<AC,đường trung tuyến AM. Trên tia đối của tia AM lấy điểm D sao cho M là trung điểm AD.
a) chứng minh tam giác MAB= tam giác MDC và DC song song với AB
b) gọi K là trung điểm AC. Chứng minh tam giác BKD cân
c) DK cắt BC tại O. Chứng minh CO=2/3CM
d) BK cắt AD tại N. Chứng minh MK vuông góc với NO

a, Xét tam giác `ADC` và tam giác `MDB` có:
`DB=DC` `(g``t)`
\(\widehat{MDB}=\widehat{ADC}\) (2 góc đối đỉnh)
`DM=DA` `(g``t)`
`=>` Tam giác `ADC=` `MDB` `(c-``g-``c)`
`b,` vì tam giác `ADC=` Tam giác `MDB` (theo a)
`=> AC = BM` (2 cạnh tương ứng)
`=>` \(\widehat{ACD}=\widehat{MBD}\) (2 góc tương ứng)
mà 2 góc này nằm ở vị trí sole trong
`=> AC` //`BM` (d. hiệu nhận biết) (đpcm)
c, Vì Tam giác `ADC=` Tam giác `MDB` (theo a)
`=>`\(\widehat{DAC}=\widehat{DMB}\) (2 góc tương ứng)
Xét Tam giác `ABM` và Tam giác `MCA` có:
AM chung
\(\widehat{DAC}=\widehat{DMB}\) `(CMT)`
`BM = AC (CMT)`
`=>` Tam giác `ABM =` Tam giác `MCA (c-g-c)
d, *xl cậu câu này mình bí mất r:')