Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có: cos 2A + 2√2.cos B + 2√2.cos C = 3
⇔2cos²A - 1 + 2√2.2.cos[(B + C)/2] . cos[(B - C)/2] - 3 = 0
⇔2cos²A + 4√2.sin (A/2) . cos[(B - C)/2] - 4 = 0(1)
Ta thấy: sin(A/2) > 0 ; cos[(B - C)/2] ≤ 1
⇒VT ≤ 2cos²A + 4√2.sin(A/2) - 4
Vì tam giác ABC không tù nên 0 ≤ cos A < 1
⇒cos²A ≤ cos A
⇒VT ≤ 2cos A + 4√2.sin(A/2) - 4
⇒VT ≤ 2.[1 - 2.(sin A/2)²] + 4√2.sin(A/2) - 4
⇒VT ≤ -4.(sin A/2)² + 4√2.sin(A/2) - 2
⇒VT ≤ -2(√2.sin A/2 - 1)² ≤ 0(2)
Kết hợp (1)(2) thì đẳng thức xảy ra khi tất cả các dấu = ở trên xảy ra
⇔cos [(B - C)/2] = 1 và cos²A = cos A và √2.sin A/2 - 1 = 0
⇔góc B = góc C và cos A = 0 và sin A/2 = 1/√2
⇔ góc B = góc C và góc A = 90 độ
Vậy góc A = 90 độ, góc B = góc C = 45 độ


Gọi M là trung điểm của cạnh BC ta có :
\(\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AM}=\overrightarrow{AD}\)
Mặt khác :
\(\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}\)
Theo giả thiết ta có :
\(\left|2\overrightarrow{AM}\right|=\left|\overrightarrow{CB}\right|=\left|\overrightarrow{AD}\right|\) hay \(AM=\dfrac{BC}{2}\)
Ta suy ra ABC là tam giác vuông tại A

a) \(\cos A=-\dfrac{3}{5}\Rightarrow\widehat{A}\approx126^052'\)
b) \(AB:2x+y-1=0;AC=2x-y-3=0\)
c) Phân giác trong \(AD\) có phương trình : \(y+1=0\)
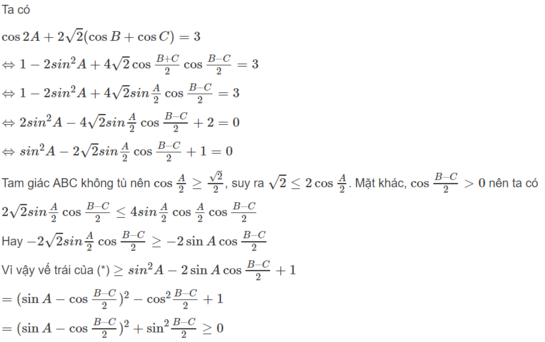
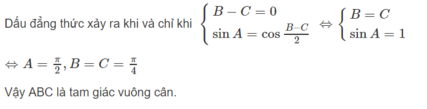
Ta có : \(cos2A+2\sqrt{2}\left(cosB+cosC\right)=3\)
\(\Leftrightarrow1-2sin^2A+2\sqrt{2}.2.cos\left(\dfrac{B+C}{2}\right).cos\left(\dfrac{B-C}{2}\right)=3\)
\(\Leftrightarrow2sin^2A-4\sqrt{2}.sin\dfrac{A}{2}.cos\left(\dfrac{B-C}{2}\right)+2=0\)
\(\Leftrightarrow sin^2A-2\sqrt{2}.sin\dfrac{A}{2}.cos\left(\dfrac{B-C}{2}\right)+1=0\)
\(\Delta\) ABC không tù nên \(cos\dfrac{A}{2}\ge cos45^o=\dfrac{\sqrt{2}}{2}\)
Suy ra : VT \(\ge sin^2A-4.cos\dfrac{A}{2}.sin\dfrac{A}{2}.cos\left(\dfrac{B-C}{2}\right)+1=K\)
Thấy : \(K=sin^2A-2.sinA.cos\left(\dfrac{B-C}{2}\right)+cos\left(\dfrac{B-C}{2}\right)^2+1-cos\left(\dfrac{B-C}{2}\right)^2\)
\(=\left(sinA-cos\left(\dfrac{B-C}{2}\right)\right)^2+sin^2\left(\dfrac{B-C}{2}\right)\ge0\)
Suy ra : \(VT\ge K\ge0=VP\)
Dấu " = " xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}sinA=cos\left(\dfrac{B-C}{2}\right)\\sin\left(\dfrac{B-C}{2}\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}sinA=cos0^o=1\\B=C\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}A=\dfrac{\pi}{2}\\B=C=\dfrac{\pi}{4}\end{matrix}\right.\) ( do \(A+B+C=\pi\) )
Vậy ...