Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

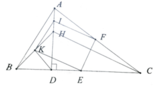
a, Chứng minh IFEK là hình bình hành có tâm O. Chứng minh IK ⊥ KE => IFEKlà hình chữ nhật => I,F,E,K cùng thuộc (O;OI)
b, Ta có: I D E ^ = 90 0 => Tam giác IDE vuông tại D
Chứng minh rằng KD ⊥ DF => ∆ KDF vuông

a) Tứ giác ACEH có
ˆACE=ˆEHA=900ACE^=EHA^=900(cùng nhìn AE)
=> tứ giác ACHE nội tiếp
b) tứ giác ACHE nội tiếp
=> ˆEAH=ˆHCEEAH^=HCE^(cùng chắn EH)
lại có ˆADF=ˆACFADF^=ACF^(cùng chắn AF)
mà ˆACF+ˆHCE=900ACF^+HCE^=900do ˆACE=900ACE^=900
=>ˆEAH+ˆADF=900EAH^+ADF^=900
=> DF⊥ABDF⊥AB
mà EH⊥ABEH⊥AB
=> DF//EHDF//EH
c)các bước chứng minh nè :
cm HOD=DCH (2 góc cùng nhìn DH)
thì => COHD nọi tiếp đường tròn thì đường tròn sẽ đi qau C H O D

a) Tứ giác ACEH có
\(\widehat{ACE}=\widehat{EHA}=90^0\)(cùng nhìn AE)
=> tứ giác ACHE nội tiếp
b) tứ giác ACHE nội tiếp
=> \(\widehat{EAH}=\widehat{HCE}\)(cùng chắn EH)
lại có \(\widehat{ADF}=\widehat{ACF}\)(cùng chắn AF)
mà \(\widehat{ACF}+\widehat{HCE}=90^0\)do \(\widehat{ACE}=90^0\)
=>\(\widehat{EAH}+\widehat{ADF}=90^0\)
=> \(DF\perp AB\)
mà \(EH\perp AB\)
=> \(DF//EH\)
c)các bước chứng minh nè :
cm HOD=DCH (2 góc cùng nhìn DH)
thì => COHD nọi tiếp đường tròn thì đường tròn sẽ đi qau C H O D
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC
Trong (O) có BC là dây cung không đi qua O có D là trung điểm BC
\(\Rightarrow OD\bot BC\)
Tương tự \(\Rightarrow\left\{{}\begin{matrix}OE\bot AC\\OF\bot AB\end{matrix}\right.\)
Ta có: \(\angle ODB+\angle OFB=90+90=180\Rightarrow OFBD\) nội tiếp
Tương tự \(\Rightarrow OECD,OEAF\) nội tiếp
\(\Rightarrow\left(AFE\right),\left(BFD\right),\left(CDE\right)\) cùng đi qua điểm O là tâm đường tròn ngoại tiếp tam giác ABC
Xét \(\Delta ABC\) có E,F lần lượt là trung điểm AC,AB
\(\Rightarrow\) EF là đường trung bình \(\Rightarrow EF=\dfrac{1}{2}BC\)
Tương tự \(\Rightarrow\left\{{}\begin{matrix}DF=\dfrac{1}{2}AC\\DE=\dfrac{1}{2}AB\end{matrix}\right.\)
Xét \(\Delta AFE\) và \(\Delta FBD:\) Ta có: \(\left\{{}\begin{matrix}AF=BF\\AE=FD=\dfrac{1}{2}AC\\FE=BD=\dfrac{1}{2}BC\end{matrix}\right.\)
\(\Rightarrow\Delta AFE=\Delta FBD\left(c-c-c\right)\Rightarrow\left(AFE\right)=\left(FBD\right)\)
Tương tự \(\Rightarrow\left(CDE\right)=\left(AFE\right)\Rightarrow\left(AFE\right)=\left(FBD\right)=\left(CDE\right)\)
thanks