Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn viết sai đề chỗ "kẻ AH vuông góc với AC (H thuộc BC)", phải là"vuông góc với BC.
A C B H 6cm 8cm 4,5cm
Theo định lí Py-ta-go, ta có:+) AB2 = BH2 + AH2 = 4,52 + 62 = 20,25 + 36 = 56,25 (cm)
+) BC2 = CH2 + AH2 =82 + 62 = 64 + 36 = 100 (cm)
=> AB2 + AC2 = 56,25 + 100 = 156,25 (cm)
Lại có: BC = BH + CH = 4,5 + 8 = 12,5=>BC2=12,52=156,25(cm)
Do đó: BC2 = AB2 + AC2 (=156,25)
Áp dụng định lí Py-ta-go đảo => tam giác ABC vuông tại A.
Vậy tam giác ABC vuông tại A
Trần Duy Thanh, chỗ \(12,6^2\) phải là \(12,5^2\) mới đúng

A B C 8 cm 6 cm 10 cm H
\(\text{Ta có: BC là cạnh lớn nhất }\)
\(\text{Mà }\sqrt{AB^2+AC^2}=\sqrt{8^2+6^2}=10\)
\(\text{Vậy tam giác ABC là tam giác vuông tại A}\)
b.Anh tính theo 2 cách nhé nhưng em chọn cách nào cx dc..
\(\text{C1}:\)\(\text{Áp dụng định lý PTG vào tam giác AHB}\)
\(AH=\sqrt{AB^2-HB^2}=\sqrt{8^2-\left(6,4\right)^2}=4,8\)
\(\text{Vậy S ABC là}:\frac{1}{2}.AH.BC=\frac{1}{2}.4,8.10=24\)
\(\text{C2}\)
\(\text{C2 đơn giản hơn k cần dùng câu b cx dc}\)
Vì ABC là tam giác vuông nên
\(\text{S ABC}=\frac{1}{2}AB.AC=\frac{1}{2}.6.8=24\)
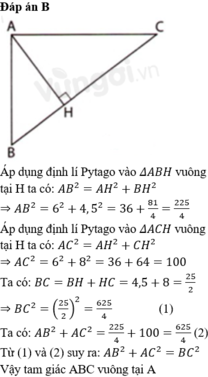
A B H C 4,5 8 6
Xét \(\Delta AHB\) vuông tại H có :
\(AB^2=AH^2+BH^2\) (Định lí PYTAGO)
=> \(AB^2=6^2+4,5^2\)
=> \(AB^2=56,25\)
=> \(AB=\sqrt{56,25}=7,5\) (cm)
Xét \(\Delta AHC\perp H\) có :
\(AC^2=AH^2+HC^2\) (Định lí PYTAGO)
=> \(AC^2=6^2+8^2\)
=> \(AC^2=100\)
=> \(AC=\sqrt{100}=10\left(cm\right)\)
Áp dụng định lí PYTAGO đảo vào \(\Delta ABC\) , ta có :
\(AB^2+AC^2=BC^2\)
=> \(7,5^2+10^2=156,25\)
=> \(BC^2=12,5\)
Vậy tam giác ABC là tam giác vuông (đpcm)
Cảm ơn bn nha.