Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TenAnh1
TenAnh1
A = (-4.34, -5.84)
A = (-4.34, -5.84)
A = (-4.34, -5.84)
B = (11.02, -5.84)
B = (11.02, -5.84)
B = (11.02, -5.84)
Hình thoi nhận O là tâm đối xứng.
\(\left|x_A\right|=\left|x_C\right|=2AC\)\(\Rightarrow\left|x_A\right|=\left|x_C\right|=8:2=4\).
Do \(\overrightarrow{OC}\) và \(\overrightarrow{i}\) cùng hướng nên \(x_C=4;x_A=-4\).
A, C nằm trên trục hoành nên \(y_A=y_C=0\).
Vậy \(A\left(-4;0\right);C\left(4;0\right)\).
\(\left|y_B\right|=\left|y_D\right|=2BD\)\(\Rightarrow\left|y_B\right|=\left|y_D\right|=6:2=3\).
Do \(\overrightarrow{OB}\) và \(\overrightarrow{j}\) cùng hướng nên \(y_B=3;y_D=-3\).
B, D nằm trên trục tung nên \(x_B=x_D=0\).
Vậy \(B\left(0;3\right);D\left(0;-3\right)\).
b) \(x_I=\dfrac{x_B+x_C}{2}=\dfrac{0+4}{2}=2\); \(y_I=\dfrac{y_B+y_C}{2}=\dfrac{3+0}{2}=\dfrac{3}{2}\).
Vậy \(I\left(2;\dfrac{3}{2}\right)\).
\(x_G=\dfrac{x_A+x_B+x_C}{3}=\dfrac{-4+0+4}{3}=0\).
\(y_G=\dfrac{y_A+y_B+y_C}{3}=\dfrac{0+3+0}{3}=1\).
Vậy \(G\left(0;1\right)\).
c) I' đối xứng với I qua tâm O nên \(I'\left(-2;-\dfrac{3}{2}\right)\).
d) \(\overrightarrow{AC}\left(8;0\right);\overrightarrow{BD}\left(0;-6\right);\overrightarrow{BC}\left(4;-3\right)\).

TenAnh1
A = (-4.3, -5.94)
A = (-4.3, -5.94)
A = (-4.3, -5.94)
B = (11.06, -5.94)
B = (11.06, -5.94)
B = (11.06, -5.94)
Do các tam giác OAB, OCD, OED, OEF, OFA , OBC cùng là tam giác đều nên OA = OB = OC = OD = OE = OF = 6cm.
Do \(\overrightarrow{i}\) và \(\overrightarrow{OD}\) cùng hướng nên D(6;0), A (0;-6).
Áp dụng hệ thức lượng trong tam giác vuông ta được:\(EC=2.DC.sin60^o=2.6.\dfrac{\sqrt{3}}{2}=6\sqrt{3}\).
\(\overrightarrow{EC}\) cùng hướng với \(\overrightarrow{j}\) nên:
Suy ra \(y_B=y_C=3\sqrt{3}\); \(y_E=y_F=-3\sqrt{3}\).
Do BC = 6cm và BC // OD nên \(x_E=x_C=3;x_F=x_B=-3\).
Vậy \(A\left(-6;0\right);D\left(6;0\right);B\left(-3;3\sqrt{3}\right),C\left(3;3\sqrt{3}\right)\);\(E\left(3;-3\sqrt{3}\right)\)\(F\left(-3;-3\sqrt{3}\right)\) .

Đặt \(\overrightarrow{PB}=x\overrightarrow{BC}\)
\(\overrightarrow{PM}=\overrightarrow{PB}+\overrightarrow{BM}=x.\overrightarrow{BC}-\dfrac{1}{3}\overrightarrow{AB}\)
\(\overrightarrow{PN}=\overrightarrow{PC}+\overrightarrow{CN}=\left(x+1\right)\overrightarrow{BC}-\dfrac{1}{2}\overrightarrow{AC}=\left(x+1\right)\overrightarrow{BC}-\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{BC}\right)\)
\(=\left(x+\dfrac{1}{2}\right)\overrightarrow{BC}-\dfrac{1}{2}\overrightarrow{AB}\)
P, M, N thẳng hàng \(\Rightarrow\dfrac{x+\dfrac{1}{2}}{x}=\dfrac{\dfrac{1}{2}}{\dfrac{1}{3}}\Rightarrow x=1\) \(\Rightarrow\overrightarrow{PB}=\overrightarrow{BC}\)
\(\Rightarrow\) B là trung điểm PC \(\Rightarrow P\left(-6;5\right)\)
Nếu bạn chưa học bài pt đường thẳng thì làm cách trên, còn học rồi thì đơn giản là thiết lập 2 pt đường thẳng BC và MN là xong

a) Ta có: \(\overrightarrow {OM} = \left( {2;1} \right),\overrightarrow {MN} = \left( { - 3;2} \right),\overrightarrow {MP} = \left( {2;1} \right)\)
b) Ta có: \(\overrightarrow {MN} .\overrightarrow {MP} = - 3.2 + 2.1 = - 4\)
c) Ta có: \(MN = \left| {\overrightarrow {MN} } \right| = \sqrt {{{\left( { - 3} \right)}^2} + {2^2}} = \sqrt {13} ,MP = \left| {\overrightarrow {MP} } \right| = \sqrt {{2^2} + {1^2}} = \sqrt 5 \)
d) Ta có: \(\cos \widehat {MNP} = \frac{{\overrightarrow {MN} .\overrightarrow {MP} }}{{\left| {\overrightarrow {MN} } \right|.\left| {\overrightarrow {MP} } \right|}} = \frac{- 4}{{\sqrt {13} .\sqrt 5 }} = \frac{- 4}{{\sqrt {65} }}\)
e) Tọa độ trung điểm I của đoạn NP là: \(\left\{ \begin{array}{l}{x_I} = \frac{{{x_N} + {x_P}}}{2} = \frac{3}{2}\\{y_I} = \frac{{{y_N} + {y_P}}}{2} = \frac{5}{2}\end{array} \right. \Leftrightarrow I\left( {\frac{3}{2};\frac{5}{2}} \right)\)
Tọa độ trọng tâm G của tam giác MNP là: \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_M} + {x_N} + {x_P}}}{3}\\{y_G} = \frac{{{y_M} + {y_N} + {y_P}}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_G} = \frac{5}{3}\\{y_C} = 2\end{array} \right. \Leftrightarrow G\left( {\frac{5}{3};2} \right)\)

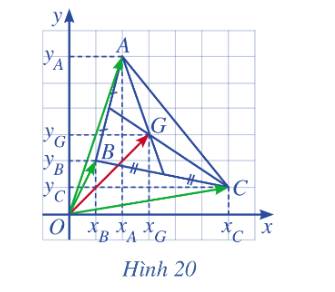
a) Ta có vectơ \(\overrightarrow {OG} \) theo ba vectơ \(\overrightarrow {OA} \) , \(\overrightarrow {OB} \)và \(\overrightarrow {OC} \) là: \(\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)\)
b) Do tọa độ ba điểm A , B và C là: \(A\left( {{x_A},{y_A}} \right),B\left( {{x_B},{y_B}} \right),C\left( {{x_C},{y_C}} \right)\) nên ta có:\(\overrightarrow {OA} = \left( {{x_A},{y_A}} \right),\overrightarrow {OB} = \left( {{x_B},{y_B}} \right),\overrightarrow {OC} = \left( {{x_C},{y_C}} \right)\)
Vậy\(\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right) = \frac{1}{3}\left( {{x_A} + {x_B} + {x_C};{y_A} + {y_B} + {y_C}} \right) = \left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)\)
Tọa độ điểm G chính là tọa độ của vectơ \(\overrightarrow {OG} \) nên tọa độ G là \(G\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)\)

TenAnh1 TenAnh1 A = (-4.3, -5.94) A = (-4.3, -5.94) A = (-4.3, -5.94) B = (11.06, -5.94) B = (11.06, -5.94) B = (11.06, -5.94) C = (-4.34, -5.84) C = (-4.34, -5.84) C = (-4.34, -5.84) D = (11.02, -5.84) D = (11.02, -5.84) D = (11.02, -5.84)
\(OB=OC=\dfrac{a}{2}\).
\(OA=\sqrt{BC^2-OC^2}=\sqrt{a^2-\left(\dfrac{a}{2}\right)^2}=\dfrac{a\sqrt{3}}{2}\).
Vậy \(C\left(\dfrac{a}{2};0\right);B\left(-\dfrac{a}{2};0\right);A\left(0;\dfrac{a\sqrt{3}}{2}\right)\).
b) \(x_E=\dfrac{x_A+x_C}{2}=\dfrac{a}{4}\); \(y_E=\dfrac{y_A+y_C}{2}=\dfrac{a\sqrt{3}}{4}\).
Vậy \(E\left(\dfrac{a}{4};\dfrac{a\sqrt{3}}{4}\right)\).
c)Do tam giác ABC đều cạnh a nên tâm đường tròn ngoại tiếp chính là trọng tâm tam giác ABC.
\(x_I=\dfrac{x_A+x_B+x_C}{3}=0\);
\(y_I=\dfrac{x_A+y_B+y_C}{3}=\dfrac{a\sqrt{3}}{6}\).
Vậy \(I\left(0;\dfrac{a\sqrt{3}}{6}\right)\).