Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D H E O
a/ Ta góc góc ACD chắn nửa cung AD là đường kính của (O)
=> góc ACD = 90 độ => CD vuông góc AC
Mà BH vuông góc với AC => BH // CD
b/ Tương tự ta cũng chứng minh được CH // BD
Từ câu a) có BH // CD => BHCD là hình bình hành
c/ Áp dụng công thức tính diện tích tam giác : \(S_{ABC}=\frac{1}{2}.AC^2.\frac{sinA.sinC}{sinB}=\frac{1}{2}.5^2.\frac{sin60^o.sin45^o}{sin75^o}=\frac{75-25\sqrt{3}}{4}\) (cm2)

A B C M N O S D H E F K P Q I J
a) Ta thấy \(\widehat{AMN}=\widehat{ABH}+\frac{1}{2}\widehat{BHQ}=\widehat{ACH}+\frac{1}{2}\widehat{CHP}=\widehat{ANM}\). Suy ra \(\Delta AMN\) cân tại A.
b) Dễ thấy tứ giác BEFC và BQPC nội tiếp, suy ra \(\widehat{HEF}=\widehat{HCB}=\widehat{HPQ}\), suy ra EF || PQ
Hiển nhiên \(OA\perp PQ\). Do đó \(OA\perp EF.\)
c) Gọi MK cắt BH tại I, NK cắt CH tại J, HK cắt BC tại S.
Vì A,K là trung điểm hai cung MN của (AMN) nên AK là đường kính của (AMN)
Suy ra \(MK\perp AB,NK\perp AC\)hay MK || CH, NK || BH
Ta có \(\Delta BHQ~\Delta CHP\), theo định lí đường phân giác và Thales thì:
\(\frac{IH}{IB}=\frac{MQ}{MB}=\frac{NP}{NC}=\frac{JH}{JC}\). Suy ra IJ || BC
Cũng từ MK || CH, NK || BH suy ra HIKJ là hình bình hành hay HK chia đôi IJ
Do vậy HK chia đôi BC theo bổ đề hình thang. Vậy HK đi qua S cố định.
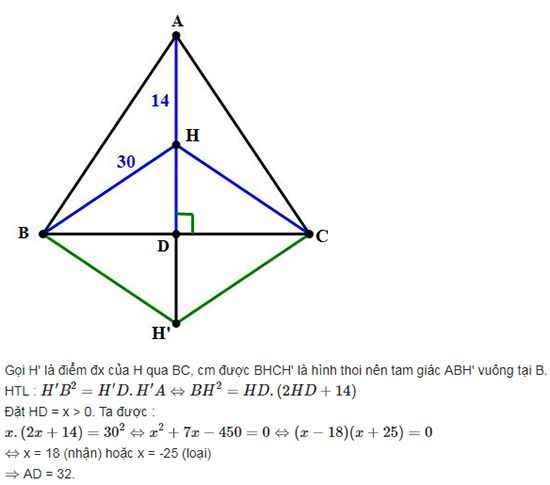
Kéo dài AD cắt đường tròn ngoại tiếp ABC tại H'.
Đặt x=HD;
Vì góc BAC nhọn và do H' đối xứng với H qua BC nên ta có: DH'=HD=x; CH'=CH=30
Áp dụng Pitago cho tg vuông ACH':
AC^2+(CH')^2=(AH')^2 -->AC^2+900=(14+2x)^2 (*)
Mặt khác CD^2= AD.DH' --> CD^2=(14+x).x (**)
trừ 2 vế (*) và (**):
AC^2+900-CD^2 =(14+2x)^2 -(14+x).x (***)
Mà AC^2-CD^2 =AD^2 =(14+x)^2;
Thế vào (***) ta được ph.tr:
(14+x)^2+900 =(14+2x)^2-(14+x)x ---> x^2+7x-450=0
phtr trên có nghiệm x= -25 (loại) và x= 18 (nhận)
AD= 14+x =14+18= 32 cm