Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn D
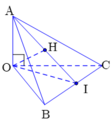
Từ giả thiết suy ra: ΔABC cân tại A có:
Gọi I là trung điểm của BC ⇒ A I ⊥ B C
Giả sử H là trực tâm của tam giác ABC.
Ta thấy O A ⊥ O B C
Vì O B ⊥ O A C ⇒ O B ⊥ A C và A C ⊥ B H nên A C ⊥ O B H ⇒ O H ⊥ A C ( 1 )
B C ⊥ O A I ⇒ O H ⊥ B C ( 2 )
Từ (1) và (2) suy ra O H ⊥ A B C
Có O I = 1 2 B C = a 2 2 = O A
=> ΔAOI vuông cân tại O => H là trung điểm AI và O H = 1 2 A I = a 2
Khi đó:
Vậy mặt phẳng (ABC) luôn tiếp xúc mặt cầu tâm O, bán kính R = 2.
Đáp án D
Từ giả thiết ta thấy 
và OBC là tam giác vuông nên thể tích cần tìm là:
VO.ABC = 1 3 OA.SOBC = 1 6 OA.OB.OC = abc 6
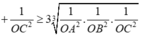
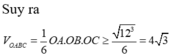
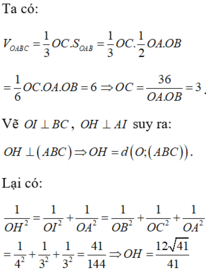
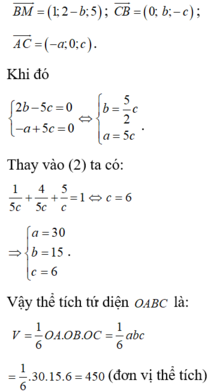
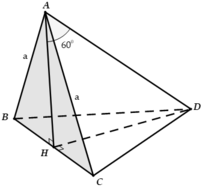
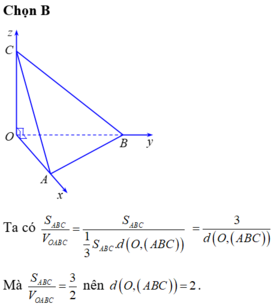
Tam giác ABC đều \(\Rightarrow OA=OB=OC\)
\(\Rightarrow\) Các tam giác OAB; OBC; OAC vuông cân tại O
\(\Rightarrow OA=OB=OC=\frac{AB}{\sqrt{2}}=a\)
\(V=\frac{1}{6}OA.OB.OC=\frac{a^3}{6}\)