Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

G B A P N M C
Ta lần lượt có:
- Trong \(\Delta ABC\)vuông tại A, suy ra:
\(BC^2=AB^2+AC^2=12^2+16^2=400\Leftrightarrow BC=20cm.\)
Ta có:
\(GA=\frac{2}{3}AM=\frac{2}{3}.\frac{1}{2}BC=\frac{1}{3}.20=\frac{20}{3}cm.\)
- Trong \(\Delta ABN\)vuông tại A, suy ra:
\(BN^2=AB^2+AN^2=12^2+8^2=208\Leftrightarrow BN=\sqrt{208}\left(cm\right)\)
Khi đó:
\(GB=\frac{2}{3}BN=\frac{2}{3}\sqrt{208}=\frac{2\sqrt{208}}{3}=\frac{8}{3}\sqrt{13}\left(cm\right)\)
- Trong \(\Delta ACP\)vuông tại A, suy ra:
\(CP^2=AC^2+AP^2=16^2+6^2=292\Leftrightarrow CP=\sqrt{292}\left(cm\right)\)
Khi đó:
\(GC=\frac{2}{3}CP=\frac{2}{3}\sqrt{292}=\frac{2\sqrt{292}}{3}=\frac{4}{3}\sqrt{73}cm.\)
Suy ra:
\(GA+GB+GC=\frac{20}{3}+\frac{8}{3}\sqrt{13}+\frac{4}{3}\sqrt{73}=\frac{4}{3}\left(5+2\sqrt{13}+\sqrt{73}\right)\left(cm\right)\)

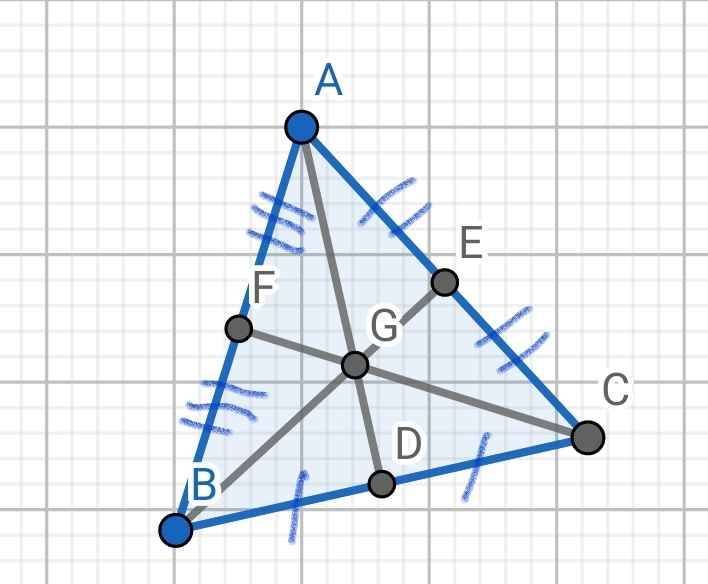
a) Do ∆ABC đều
⇒ AB = AC = BC và ∠A = ∠B = ∠C = 60⁰
Do AD, BE, CF là ba đường trung tuyến
⇒ F, E, D lần lượt là trung điểm của AB, AC, BC
⇒ AF = BF = AE = CE = BD = CD
Xét ∆BEC và ∆CFB có:
CE = BF (cmt)
BC chung
∠BCE = ∠CBF = 60⁰
⇒ ∆BEC = ∆CBF (c-g-c)
⇒ BE = CF (hai cạnh tương ứng) (1)
Xét ∆ADC và ∆CFA có:
AC chung
CD = AF (cmt)
∠ACD = ∠CAF = 60⁰
⇒ ∆ADC = ∆CFA (c-g-c)
⇒ AD = CF (hai cạnh tương ứng) (2)
Từ (1) và (2) ⇒ AD = BE = CF (3)
b) Do AD là đường trung tuyến ứng với đỉnh A
⇒ AG = 2/3 AD (4)
Do BE là đường trung tuyến ứng với đỉnh B
⇒ BG = 2/3 BE (5)
Do CF là đường trung tuyến ứng với đỉnh C
⇒ CG = 2/3 CF (6)
Từ (3), (4), (5), (6) ⇒ AG = BG = CG

a:BE=AE=AB/2
CD=CA/2
mà AB=CA
nên BE=CD
Xét ΔBEC và ΔCDB có
BE=CD
góc EBC=góc DCB
BC chung
Do đó:ΔBEC=ΔCDB
b: Xét ΔBGC có \(\widehat{GBC}=\widehat{GCB}\)
nên ΔGBC cân tại G

Ngày mai mình nộp bài rồi, mong các bạn chỉ bài giúp mình . mình không hiểu gì về 2 bài toán này cả TT_TT

Xét hai tam giác vuông ABC và tam giác vuông CBD ta có:
góc B chung
góc BAC= góc BCD(=900)
=> tam giác ABC đồng dạng tam giác CBD(g.g)
=>ABBC=ACCD=BCBD
Mà: AB=9 cm; AC=12cm
Áp dụng định lí Py-ta-go trong tam giác vuông ABC ta có:
BC2=AC2+AB2
⇔BC2=122+92
⇔BC=√225
⇒BC=15
Ta có: ABBC=ACCD⇔915=12CD⇔CD=15×129
⇒CD=20(cm)
Vậy CD= 20cm